This post is meant specifically for students in APMA E2000 at Columbia, particularly regarding the particulars of submission, but others may take or leave what they like.
Set up your space
Setting up one’s workspace of course is of course a matter of personal preference, and you should always do what works. What follows are recommendations that will hopefully make the material ‘stick’ better.
Start by obtaining 3 things from you preferred stationery/office supply store:
- A stack of legal pads
- A ream of printer paper
- A good pen or pencil (but not too good)
Set the legal pad up front and center of your workspace. This is where mathematics is done. That is, it is for solving problems. The printer paper is for writing solutions. this is a different task and must be kept separate.
Have access to:
- A copy of the assignment
- Your class notes
- The textbook
- A calculator or CAS you are familiar with.
This last one is not essential for this class, but can be very helpful for visualization of objects, which can be difficult, and for checking your answer. Nota bene I highly recommend turning off the WiFi.
Prepare mentally
I am not suggesting doing mathematics requires ample stretching or elaborate breathing exercises (though you are welcome to try that), but one should repeatedly ask oneself in this course, “What have we been doing?”
The more frequently you practice getting your brain into a particular gear, the easier it will be to shift come exam time. Just don’t wear out the clutch-plate, or this metaphor.
For example, you are sitting down to do a Calculus II problem set. Take a glance at the assignment, but before diving into any problem tell yourself what the broader subject is all about.
Ah. Representing functions as power series. that’s where essentially we write a function \(f(x)\) as a giant polynomial. It basically comes down to finding coefficients, the numbers in front of \(x^n\)’s.
Furthermore, set modest goals. “I’m going to work for a solid hour.” “I’m going to do two problems.” Breaking a homework set into multiple sessions makes it less arduous and necessitates more of that “shifting gears” practice.
Do the math
Of course, this is the hard part, that I cannot write a pithy guide for. Problem-solving is too complex and art to be boiled down to a fixed set of rules. The principal goal of a course like this is to develop those skills over time.
Nevertheless, let’s walk through an example.
Example 1
- Evaluate the following indefinite integral as a power series. \[\int \frac{e^x - 1}{x}\,dx \]
Start by transcribing the problem to your scrap paper in your own, informal way. Next, write down the form them answer will take. This gives you a goal to aim for. In more complex problems, it is easy to lose sight of this goal. Keep it boxed on your paper as an easy reference.
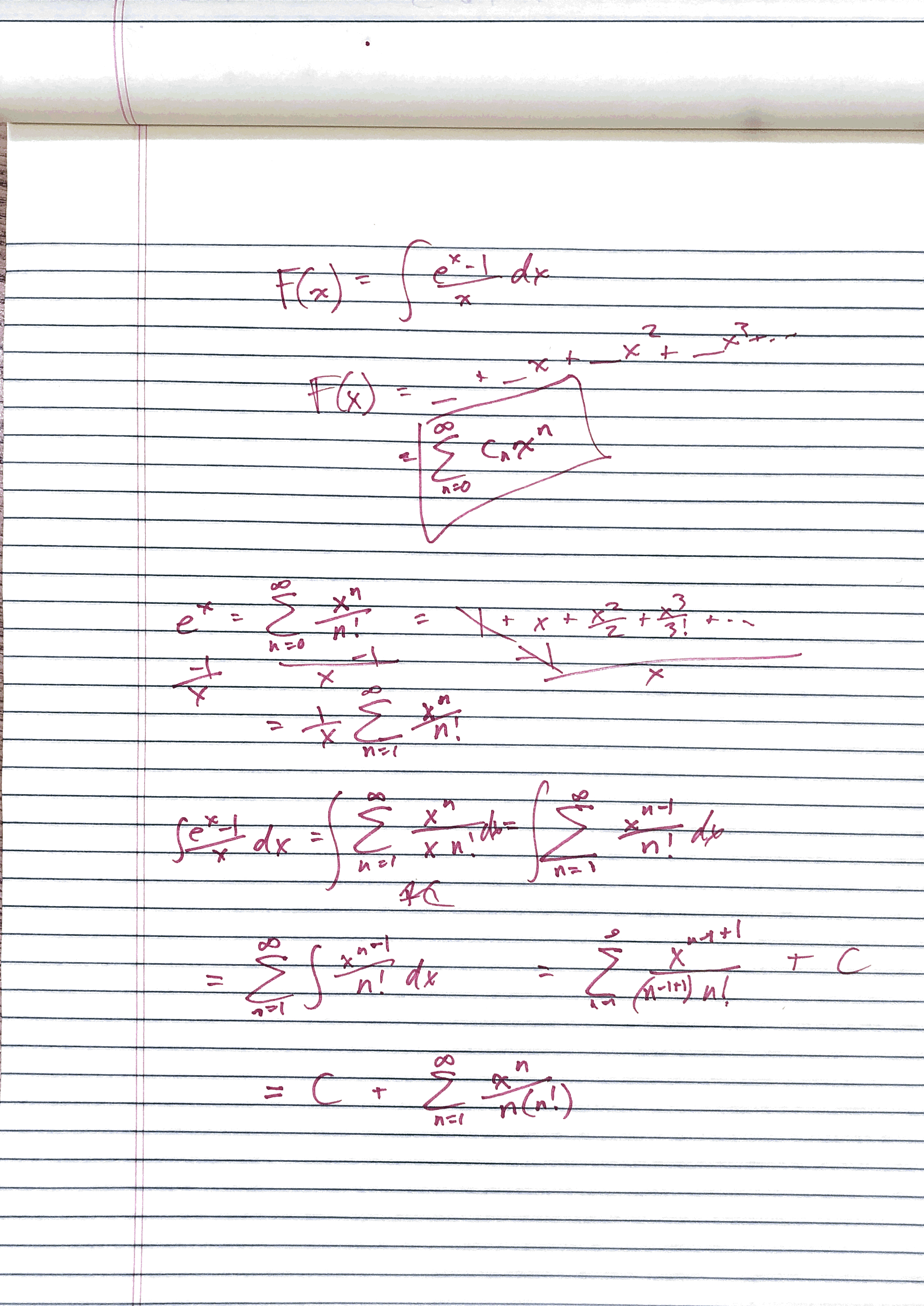
This is way neater than most of my scratch-work looks. It almost could be submitted, but note that in working out the power series for \(\frac{e^x-1}{x}\), I did calculations on top of old work. Do not turn the grader into an archaeologist. They need not scrape back layers to see how you arrived at your conclusion.
Check it
Now is a good time to check in with Mathematica, Sage, your calculator, etc.

Don’t jump to this step to quickly. The point of exercises is to have your mind work these things out.
Write it up
This step serves many purposes. It is not meant as a historical record of how you solved the problem but a rather a justification of your answer. Remove the extraneous but leave enough information that one of your peers could follow from the problem’s statement to its conclusion smoothly.

Scan it
Get yourself a real document-scanning app on your phone. The Gradescope Scanning Guide has some suggestions but there are many more listicles out there.
Remember For each assignment, make 1 PDF file with 1 page per question. This will make for neater work, make submission to Gradescope easier, and
Remember:
Revisit it
Don’t let the first time you do a problem be the last time you think about it. Part of your studying should be looking at your old work and calling to mind not only how to do it, but what knowledge was required to do it, and perhaps most importantly, what was the point of doing it? What ideas was it meant to enforce?