Lecture 14     

Integrals

APMA E2000

Drew Youngren dcy2@columbia.edu

$\gdef\RR{\mathbb{R}}$ $\gdef\vec{\mathbf}$ $\gdef\bv#1{\begin{bmatrix} #1 \end{bmatrix}}$ $\gdef\proj{\operatorname{proj}}$ $\gdef\comp{\operatorname{comp}}$

Announcements

  • HW8 due after break
  • Quiz 5 this week (opens Wednesday)
    • Local min/max
    • Optimization

1-minute review

Theorem

A continuous function on a closed and bounded set $D$ must achieve its absolute minimum and maximum.

The upshot is:
  • Find critical points on interior of $D$.
  • Find Lagrange points on boundary of $D$.
  • Choose least/greatest value of $f$ on combined list.

Definite Integrals

Recall

\[\int_a^b f(x)\,dx = \lim_{N\to \infty} \sum_{i=1}^{N} f(x_i^*)\,\Delta x \] where $x_i^*$ is a sample point in the $i$th interval and $\Delta x = \frac{b - a}{N}$.

Example

Multiple Integration

What questions can integrals answer?
  • What is the volume of air in a circus tent?
  • What are the chances a dart thrown at a bullseye lands on triple-20?
  • What is the average temperature in this room?
Definition

A double integral over a region $\mathcal R \subset \RR^2$ of a scalar field $f(x,y)$ is a limit of Riemann sums \[\iint\limits_{\mathcal R} f\,dA = \lim\limits_{M,N \to \infty} \sum_{i = 1}^M \sum_{j=1}^N f(x_{ij}^*, y_{ij}^*)\,\Delta A_{ij} \] where $(x_{ij}^*, y_{ij}^*)$ is a sample point in, and $ \Delta A_{ij}$ the area of, the $(i,j)$th subrectangle inside $\mathcal R$.

Graphically, this is the signed volume under the graph of the function.

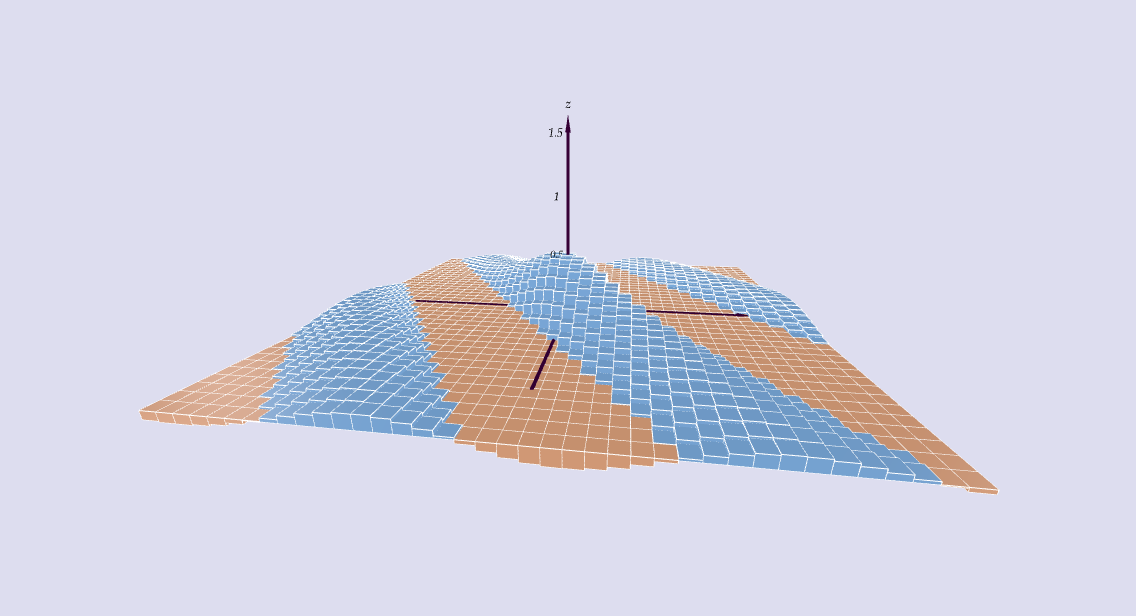
Cuboids approximating volume under a graph.

Iterated Integrals

Poll
Iterated Integrals

Over a rectangle $[a,b]\times [c,d] \subset \RR^2$, we define the iterated integral \[ \int_a^b \int_c^d f(x,y)\,dy\,dx = \int_a^b \left(\int_c^d f(x,y)\,dy\right)\,dx\]

Iterated Integrals
Fubini's Theorem

If $f$ is continuous on rectangle $\mathcal R = [a,b]\times [c,d]$, then \[ \iint\limits_{\mathcal R} f\,dA =\int_a^b \int_c^d f(x,y)\,dy\,dx = \int_c^d \int_a^b f(x,y)\,dx\,dy. \]

Example

Let $\mathcal{R} = [0,\pi]\times[0,2\pi]$. Evaluate \[\iint_\mathcal{R} x \cos(xy)\,dA\] as an iterated integral.

\[\int_0^{2\pi} x \cos (xy)\,dy = \sin (xy)\Big\vert_{0}^{2\pi} = \sin 2\pi x \] \[\int_0^{\pi} \sin 2\pi x \,dx = \frac{1}{2\pi} \left( 1 - \cos (2\pi^2) \right) \]
Non-rectangular domains

A region in $\RR^2$ that is bounded by graphs of functions (of one variable) can be integrated over as interated integrals.

Suppose $\mathcal{D} = \{(x,y) \mid g(x) \leq y \leq h(x) \}$. Then

\[\iint_\mathcal{R} f(x,y) \,dA = \int_a^b \int_{g(x)}^{h(x)} f(x,y)\,dy\,dx\]

Example

Let $\mathcal D$ be the region bounded by the curves $y = \frac{x^3}{32}$ and $y = \sqrt{x}$. Write $\iint\limits_{\mathcal D} f\,dA$ as an iterated integral.

Solution

\[ \int_0^4 \int_{x^3/32}^{\sqrt{x}} f(x,y) \,dy\,dx \]

\[= \int_0^2 \int_{y^2}^{\sqrt[3]{32 y}} f(x,y) \,dx\,dy \]

Example

Find the volume of the solid region under the plane
$x-2y+z=10$ and above the region bounded by
$x+y=1$ and $x^2+y=1$.

  1. Sketch region of integration.
  2. Select order of integration.
  3. Set up iterated integral.

Solution. \[ \int_{0}^1 \int_{1-x}^{1 - x^2} (10 - x + 2y)\,dy\,dx \] \[ = \frac{107}{60} \]

Triple Integrals

Definition

Integrating in three dimensions presents no theoretical challenge. \[\iiint_E f(x,y,z)\,dV = \]\[\lim_{M,N,P\to\infty} \sum_{i=1}^M\sum_{j=1}^N\sum_{k=1}^P f(x_{ijk}^*,y_{ijk}^*,z_{ijk}^*)\,\Delta V_{ijk}\]

Triple Integrals

Fubini's Theorem applies directly to this case; thus, we can compute using (3) iterated integrals. \[ \iiint_E f(x,y,z)\,dV = \]\[ \int_a^b \int_{g(x)}^{h(x)} \int_{j(x,y)}^{k(x,y)} f(x,y,z)\,dz\,dy\,dx \]

Example

Set up an iterated integral to find the volume of the solid region $S$ in the first octant with \[x^2 + y^2 \leq z \leq 4.\]

Solution \[ \operatorname{Vol}(S) = \iiint\limits_S 1\, dV = \int_0^2 \int_0^{\sqrt{4 - x^2}} \int_{x^2 + y^2}^4 \,dz\,dy\,dx = 2\pi \]

Bonus

Suppose a point $(x,y,z)$ is selected randomly from $S$ above. What is the probability that $x > 1$?

Solution

Simply find the proportion of the region (by volume) that has the property $x > 1$.

\[ P(x > 1) = \frac{\int_1^2 \int_0^{\sqrt{4 - x^2}} \int_{x^2 + y^2}^4 \,dz\,dy\,dx}{\operatorname{Vol}(S)} \approx 0.253 \]

Learning Outcomes

You should be able to...
  • Express a multiple integral as a limit of Riemann sums.
  • Detect syntactic errors in expressions of iterated integrals.
  • Set up iterated integrals (in 2 and 3 dimensions) for regions bounded by graphs of functions.
  • Given an iterated integral in 2 variables, sketch the region of integration and change the order.
  • Change the order of integration for iterated integrals in 3 dimensions for select cases.
  • Compute volumes and areas via multiple integration.