Lecture 16.5
More Applications
APMA E2000
Drew Youngren dcy2@columbia.edu
Announcements
- HW 9 due Tues.
-
Quiz 6 this week.
- Double/triple integrals
- Coordinate systems
-
Exam 2 Thurs, 04/03
- Same format as last time
- New seat assignments
- Not cumulative in the narrow sense but all math is cumulative.
1-minute review
Total Mass
\[M = \iiint_\mathcal E \mu(x,y,z)\,dV.\]
Center of Mass
\[\bv{\bar{x} \\ \bar{y} \\ \bar{z}} = \frac1M \bv{\iiint_\mathcal E x \mu(x,y, z)\,dV \\ \iiint_\mathcal E y \mu(x,y, z)\,dV \\ \iiint_\mathcal E z \mu(x,y, z)\,dV}\]
Moment of Inertia
\[ I = \iiint\limits_{\mathcal E} (\text{distance to axis})^2 \mu(x,y,z)\,dV \]
Practice
Example
The nose of a race car is modeled by half of a right cone with height $h$ and radius $R$. Assuming uniform density, how high is the center of mass from the bottom.
MoI Examples
Find an expression for the moment of inertia $I$ (about a central axis) in terms of the total mass $M$ (with uniform density) for the following shapes:
- Cube with side $2R$.
- Right cone with base radius $R$ and height $h$.
- Half-ball with radius $R$.
Solution. Cube: $M = \mu 8 R^3$. \[ I_z = \int_{-R}^{R}\int_{-R}^{R}\int_{-R}^{R}(x^2 + y^2) \mu\,dz\,dy\,dx \]\[= \mu \frac{16}{3} R^5 = \frac23 M R^2\]
Solution. Cone: $M = \mu \frac13 \pi R^2 h$. \[ I_z = \int_{0}^{2\pi}\int_{0}^{R}\int_{0}^{h - \frac{h}{R}r}(r^2) \mu r\,dz\,dr\,d\theta\] \[= \mu 2\pi \int_0^R\left(hr^3 -\frac{h}{R}r^4\right)\,dr\] \[ =\mu \frac{\pi}{10} h R^4 = \frac{3}{10} M R^2\]
Solution. Half-ball: $M = \mu \frac23 \pi R^3 $. \[ I_z = \int_{0}^{2\pi}\int_{0}^{\pi/2}\int_{0}^{R}(\rho^2 \sin^2 \phi) \mu \rho^2 \sin\phi \,d\rho\,d\phi\,d\theta\] \[ = 2\pi \mu \frac{R^5}{5}\int_0^\pi \sin^3 \phi \,d\phi = 2\pi \mu \frac{R^5}{5}\int_{-1}^0 (1 - u^2)\,du\] \[ = \frac{4\pi}{15} R^5 = \frac25 M R^2\]
Probability
Definition
A probability density on a sample space $S
\subset \RR^2$ is a scalar field $\mu(x,y) \geq 0$ such that
\[\iint_S \mu(x,y)\,dA = 1.\]
The probability of an event $E \subset S$ is \[P(E) = \iint_E \mu\,dA.\]
Example
What is the probability 2 numbers chosen randomly from $[0,1]$ have a product bigger than $\frac12$?
Solution. For uniform probability on 2 variable, $\mu(x,y) = 1$ on $[0,1]^2$. We just integrate over the region $xy \geq \frac12$.
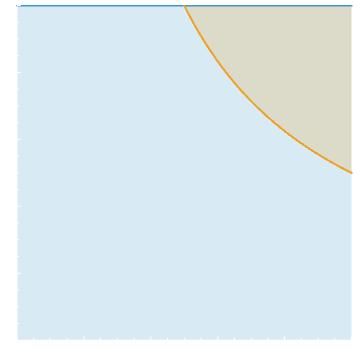
\[\int_{1/2}^1 \int_{1/(2x)}^1 \,dy\,dx = \left(x - \frac{1}{2} \ln |x|\right)\Big\vert_{1/2}^1 \approx 0.153 \]
Example
What is the probability 2 numbers chosen randomly from $[0,1]$ are more than $\frac13$ apart?
Solution. We can argue from the areas in the picture. $P(3) = \frac23 \times \frac 23 = \frac 49$.

But an alternative is to reduce the sample space to
$x < y$.
Then $\mu(x,y) = 2$. \[ P(E) = \int_0^{2/3} \int_{x + 1/3}^1
2\,dy\,dx = \frac49 \]
Example
What is the expected value of the smaller of 2 random numbers in $[0,1]$?
Solution. Expected value of random variables are exactly like centers of mass.
\[ \bar{x} = \iint_S x \mu\,dA = \int_0^1 \int_x^1 2x\,dy\,dx = \frac13 \]
Example
Three random numbers between $0$ and $1$ are chosen consecutively. What is the probabilty the third is greater than the sum of the first two?
Solution. Call the consecutive numbers $x,y,z$. The sample space is the unit cube. We just need the portion with $z > x + y$.
Plot of event and sample space.
The only tricky bit is remembering $x + y < 1$ in this event \[P(E) = \int_{0}^{1} \int_0^{1 - x} \int_{x + y}^1 dz\,dy\,dx = \frac16\]
Example
Suppose a point is chosen at random from the unit square $[0,1]^2$. What is the probability that $r < \frac{2\theta}{\pi}$ where $r$ and $\theta$ are the usual polar coordinates?
Solution. We can integrate the region easily in polar coords.

\[ P(E) = \int_0^{\pi/2} \int_0^{2\theta / \pi} r\,dr\,d\theta = \int_0^{\pi/2} \frac{2\theta^2}{\pi^2} d\theta = \frac{\pi}{12} \]
Example
Suppose a number $x$ is selected randomly from $[0,1]$ and then a number $y$ is chosen randomly from the interval $[x,1]$. What is the expected value of $y$?
Warning. This is a bit tricky.
Solution. The sample space is clearly $0 \leq x \leq y \leq 1$. Since $y$ is chosen uniformly, the probability densiity can't depend on $y$ and thus has the form $\mu(x)$, but the marginal density for $x$, must be uniform. That is, \[ \int_x^1 \mu(x)\,dy = 1\] for all $x$, or $\mu(x) = \frac{1}{1 - x}$.
\[ \bar y = \int_0^{1} \int_x^{1} \frac{y}{1-x}\,dy\,dx = \frac12\int_0^1 \frac{1 - x^2}{1 - x} \,dx = \frac34\]