Lecture 17
Vector Fields & Path Integrals
APMA E2000
Drew Youngren dcy2@columbia.edu
Announcements
-
Quiz 4 (async) 11/6
- Integrals
- HW 8 due Thurs.
-
Exam 2 Tues 11/11
- Through HW8.
- Lectures 11–17.
- Review session TBD
1-minute review
MoI Integrals
Suppose the same mass $M$ were distributed evenly over the following regions in space:
- $B$ a solid ball of radius $R$.
- $S$ a (hollow) sphere of radius $R$.
- $C$ a ring (circle) of radius $R$.
Rank their moments of inertia around a central axis from least to greatest.
For the ball $\mathcal B$:
\[ I_z = \iiint\limits_{\mathcal B} (x^2 + y^2) \mu\, dV = \] \[ \int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{R} \mu (\rho^2 \sin^2 \phi) \rho^2 \sin \phi\,d\rho\,d\phi\,d\theta \] \[ = \frac{8}{15} \mu \pi R^5 = \frac25 M R^2 \]
We Need a New Integral
Let $C$ be the (1-dimensional) ring object above \[\iiint_C f\,dV = 0\] for any $f$.
Assume a constant linear density of $\frac{M}{2\pi R} \frac{\text{unit of mass}}{\text{unit of length}}$.
\[ \int_C (\text{distance to axis})^2 \times (\text{linear density})\,d(\text{length}). \] This requires a new integral called a line integral or path integral.
Other Integrals
Framework
Every integral has three essential parts, summarized as the where, the what, and the how.
\[ \int\limits_D F\,d\omega \]- Where? the domain of integration $D$
- What? the integrand $F$
- How? the differential (form) $d\omega$
Path Integrals
Taxonomy
A line integral, also called a path integral, is an integral whose domain of integration is $C$, the image of a curve parametrized by $\vec r(t)$.
They come in different "flavors" ...
Go to 3Demos → Story → Path Integrals for a demo of the flavors.
w/ respect to arc length
\[ \int\limits_{\mathcal C} f\,ds \]-
Where? path in space $\mathcal C$
- given by $\vec r(t) = \langle x(t), y(t),\ldots \rangle$, $a \leq t \leq b$
- What? scalar field $f(x,y,\ldots)$
- How? w.r.t. arc length: $ds$
Formula
Formula
Formula
Interpretation
If $f$ is the height of a wall whose base runs along $\mathcal C$, then $\int_{\mathcal C} f\,ds$ would be the area of the wall.
N.B. Though $\int_C ds$ is always positive, $f$ could yield negative values, so $\int_C f\,ds$ can be negative.
w/ respect to a coordinate
\[ \int\limits_{\mathcal C} f\,dx \]-
Where? oriented path in space
$\mathcal C$
- given by $\vec r(t) = \langle x(t), y(t),\ldots \rangle$, $a \leq t \leq b$
- What? scalar field $f(x,y,\ldots)$
- How? w.r.t. the change in the $x$-direction: $dx$.
Formula
Formula
Formula
Interpretation
These integrals are certainly more abstract. They are most often the building blocks of vector field integrals.
N.B. Orientation of path matters here. Reversing the direction negates the integral.
Example
Let $C$ be the piece of the parabola $y=(x-1)^2$ from $(0,1)$ to $(3,4)$, and let $f(x,y) = x+y$.
Compare the line integrals: \[\int_C f\, dx, \int_C f\, dy, \text{ and } \int_C f\, ds \]
Solution
\[ \int_C f\,dx = \int_0^3 (t + (t - 1)^2)\,dt = 7.5\]
\[ \int_C f\,dy = \int_0^3 (t + (t - 1)^2) 2(t-1)\,dt = 16.5\]
\[ \int_C f\,ds = \int_0^3 (t + (t - 1)^2)\sqrt{1 + 4(t-1)^2}\,dt \approx 20.1 \]
Vector Fields
Definition
A vector field is simply a function \[ \vec F: \RR^n \to \RR^n. \]
We plot them by drawing arrows at regularly-spaces points in the domain. Here is:
\[\vec F(x,y) = \bv{\sin y \\ \cos x} \]More Examples
One common use of vector fields is the velocity field of a fluid. We picture the flow by "following the vector field".
Line Integral of a Vector Field
\[ \int\limits_{\mathcal C} \vec F \cdot\,d\vec r \]-
Where? oriented path in space
$\mathcal C$
- given by $\vec r(t) = \langle x(t), y(t),\ldots \rangle$, $a \leq t \leq b$
-
What? vector field $\vec F$
- $\vec F(x,y,\ldots) = \langle P(x,y, \ldots), Q(x,y, \ldots), \ldots \rangle$
- How? along the path: $d\vec r$
Formula
Interpretation
$\int_C \vec F\cdot d\vec r$ measures how much a vector field $\vec F$ pushes along a path $C$.
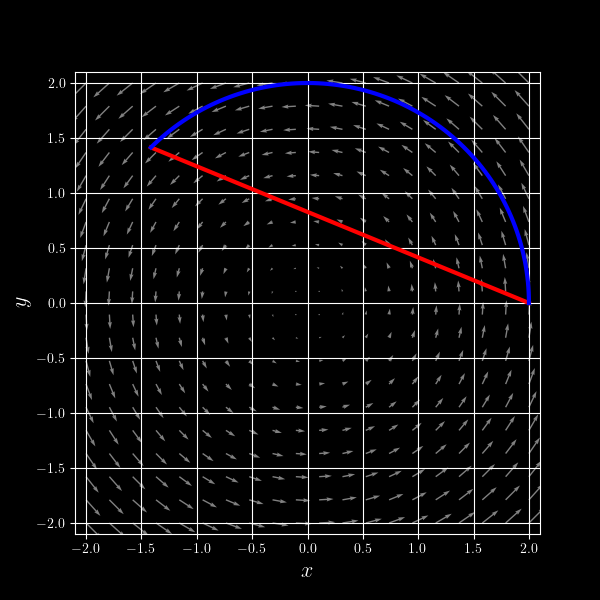
Interpretation
$\int_C \vec F\cdot d\vec r$ measures how much a vector field $\vec F$ pushes along a path $C$.
- If $\vec F$ is a force, and $C$ is the path of an object, the line integral is the work done by the force on the object.
- Consider the question of whether a marathon run was "wind-assisted."
Work Integrals
Work = Force × Distance
Suppose a particle moves along a path $C$ parametrized by $\vec r(t)$ for $a \leq t \leq b$, and is subject to a force field $\vec F$ at each point of the curve, then the total work done by the force isWork = Force × Distance
Hooke's Law: force of a spring is proportional to displacement. $F = -k x$.
Compute the work done by spring moving an object from position $x_0$ to $x_1$.
$x(t) = x_0 + (x_1 - x_0)t$ for $0\leq t \leq 1$. \[ \int_0^1 -k( x_0 + (x_1 - x_0)t) (x_1 - x_0)\,dt = \frac12kx_0^2 - \frac12 k x_1^2 \]
Example - Rolling rolling rolling
A ball falls down a parabolic ramp $y=x^2$ from $(-2,4)$ to the origin. How much work was done by gravity?
$\vec r(t) = \left\langle t, t^2 \right\rangle$ for $-2\leq t \leq 0$. \[ \int_{-2}^{0} \left\langle 0, -mg \right\rangle \cdot \left\langle 1, 2 t \right\rangle= mg4 \]
Alternate Forms
In Components
Per Arc Length
Learning Outcomes
You should be able to...
- Sketch a vector field plot, and match a plot with its formula from a list.
-
Convert path integrals of each kind to 1-dimensional integrals
via parametrization:
- w/ respect to arc length.
- w/ respect to individual coordinates.
- Identify which of these depend on orientation of the curve and how.
- Estimate sign and/or magnitude of line integrals without direct computation.
- Convert work problems into appropriate forms of line integrals.