Lecture 23      

The Divergence Theorem

APMA E2000

Drew Youngren dcy2@columbia.edu

$\gdef\RR{\mathbb{R}}$ $\gdef\vec{\mathbf}$ $\gdef\bv#1{\begin{bmatrix} #1 \end{bmatrix}}$ $\gdef\proj{\operatorname{proj}}$ $\gdef\comp{\operatorname{comp}}$

Announcements

  • HW 13 due Tuesday
  • Quiz 9
    • Surface & Flux Integrals
  • Final exam schedule released
    • See edstem announcement

1-minute review

Stokes' Theorem

Let $\Omega$ be an oriented surface in $\RR^3$ and $\partial \Omega$ its positively-oriented boundary. If $\vec F(x,y,z)$ is a smooth vector field, then \[ \iint_{\Omega} \nabla \times\vec F \cdot d \vec S = \oint_{\partial \Omega} \vec F\cdot d \vec r \]

Example

Find the flux of the curl of the vector field $2y\,\vec i + 3z\,\vec j +x\,\vec k$ through the piece of the cone $z=\sqrt{x^2 + y^2}$ below $z=2$, oriented upward.

$\operatorname{div} \mathbf F$

Positive divergence

\[ \vec F(x,y,z) = x\,\vec i + y\,\vec j + \frac12\,\vec k \]

Negative divergence

\[ \vec F(x,y,z) = \vec i + \vec j - 2z\,\vec k \]

Incompressibility

\[ \vec F(x,y,z) = \frac{x}{2}\,\vec i - y\,\vec j + \frac{z}{2}\,\vec k \]

The Divergence Theorem

Flux Example Reprise

Consider the vector field $\vec F(x,y,z) = x\,\vec i$. Consider the surfaces

  • $\Omega_1$: piece of the plane $x=0$ for $0 \leq y,z \leq 1$
  • $\Omega_2$: piece of the surface $x= 3 y (1-y)$ for $0 \leq y,z \leq 1$

oriented in the positive $x$-direction. Through which surface is the flux of $\vec F$ greater?

The Divergence Theorem

aka Gauss' Theorem

Let $E$ be a solid region in $\RR^3$ and $\partial E$ its outward-oriented boundary. If $\vec F(x,y,z)$ is a smooth vector field, then \[ \iint\limits_{\partial E} \vec F \cdot \vec N\,d S = \iiint\limits_E \nabla \cdot \vec F\,dV \]

Justification

\[\iint\limits_{\partial E} \vec F\cdot \vec N\,dS \approx \sum\Delta \text{flux} \] \[ \Delta\text{flux}_{x\text{-dir}} = \left(P\left(x + \frac{\Delta x}{2}, y, z\right) - P\left(x - \frac{\Delta x}{2}, y, z\right)\right) \Delta y\,\Delta z \] \[\approx P_x(x,y,z)\, \Delta x\,\Delta y\,\Delta z \] \[ \Delta\text{flux}_{y\text{-dir}} \approx Q_y(x,y,z)\, \Delta x\,\Delta y\,\Delta z \] \[ \Delta\text{flux}_{z\text{-dir}} \approx R_z(x,y,z)\, \Delta x\,\Delta y\,\Delta z \]

Add these together, to get \[\sum\Delta \text{flux} \approx \sum (P_x + Q_y + R_z) \, \Delta x\,\Delta y\,\Delta z \] \[ \longrightarrow \iiint\limits_E \operatorname{div} \vec F dV \]

Interpretations

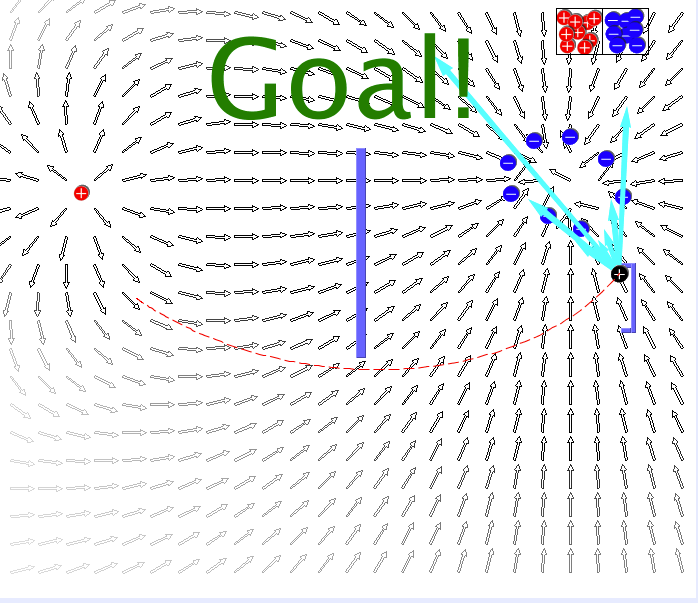
Electric Field Hockey

One of Maxwell's equations is \[\nabla \cdot \vec E = \rho \]

which says the divergence of the electric field is the charge density.

Screenshot of 'hockey' game displaying a number of charges and the associated electric field

via Ruth Chabay, et al, UC Boulder

Spraying Champagne (2015)
Spraying Champagne (2024)

photo credit: Charles Wenzelberg / New York Post

Examples

Example

Compute the flux of the radial vector field $x\,\vec i + y\,\vec j + z\,\vec k$ through the outward-oriented unit sphere.

Solution. $\nabla \cdot \langle x,y,z \rangle = 3$ \[\iint_{\partial E} \vec F\cdot dS = \iiint\limits_E 3\,dV = 4\pi \]

Example

Find the flux of the vector field $(1 - x)\,\vec i - y\, \vec j$ through the piece of the cone $z=\sqrt{x^2 + y^2}$ below $z=2$, oriented upward.

Solution. Direct computation: \[\vec r(u,v) = \bv{u \cos v \\ u \sin v \\ u} \qquad \begin{cases} 0 \leq u \leq 2 \\ 0 \leq v \leq 2 \pi \end{cases} \]

\[\iint_C \vec F\cdot d\vec S = \int_0^{2 \pi} \int_0^2 \bv{ 1 - u \cos v \\ - u \sin v \\ 0 } \cdot \bv{ -u \cos v \\ -u\sin v \\ u } du\,dv\]

\[ = \int_0^{2 \pi} \int_0^2 u^2 \,du\,dv = \frac{16\pi}{3} \]

Using Gauss': Enclose the surface by adding a flat disk $\mathcal T$ to the top, oriented up, at $z = 2$. Then, by Gauss, \[ \iint_{\mathcal T} \vec F\cdot \vec N \,dS - \iint_{\mathcal C} \vec F\cdot \vec N \,dS = \iiint_E \nabla \cdot \vec F\,dV = \iiint_E -2\,dV \] $= -2(\frac{1}{3}\pi 2^2(2)) $. Note for $\mathcal T$ the unit normal is $\vec k$ and $\vec F\cdot \vec k = 0$. Solving for the desired flux gives the answer above.

Buoyancy

Ηydrostatic pressure is proportional to depth. $P = \rho g d$. The force on a small piece of submerged surface is $-P\, \vec N\,dS$ where $\vec N$ is the normal vector to the surface. The (net) buoyant force on the hull of a watercraft is the component of this force in the upward direction.

Use the Divergence Theorem to relate the buoyant force to the volume of a submerged object.

Solution. Suppose an object is modeled by a solid $E$ with outward-oriented normal $\vec N$ on the boundary $\partial E = \Sigma$, where the surface of the water is $z = 0$.

Then the total buoyant force is \[ \iint_\Sigma \rho g (-z)(-\vec N)\cdot \vec k\, dS = \rho g \iint_{\partial E} z\,\vec k \cdot d\vec S \]

but the vector field $z\,\vec k$ has divergence 1, so the RHS is just $\rho g \operatorname{Vol}(E)$, the weight of the water displaced by $E$.

Learning Outcomes

You should be able to...
  • State the Divergence Theorem and identify its necessary components.
  • Verify both sides of the equality in the Div Thm in basic examples.
  • Exploit the Divergence Theorem to compute flux through a not-necessarily closed surface.
  • Create a specific example in which both Stokes' and Divergence Theorems apply.