Homework 1

Due: January 22, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1.   a. Let $\mathcal{S}$ be the solid region first octant bounded by the coordinate planes and the planes $x = 3$, $y = 3$, and $z = 4$ (including points on the surface of the region). Sketch, or describe the shape of the solid region $\mathcal{E}$ consisting of all points that are at most 1 unit of distance from some point in $\mathcal{S}$. Also find the volume of $\mathcal{E}$.

   b. Write an equation that describes the set of all points that are equidistant from the origin and the point $(2, -1, -2)$. What does this set look like?

2. Consider the points $A = (0, -3, -1)$ and $B = (1, 2, -2)$. Let $O$ denote the origin, $(0, 0, 0)$.

   a. Let $M$ denote the midpoint of the line segment $\overline{AB}$. Find the vector $\overrightarrow{OM}$.

   b. Let $N$ denote the point on the line segment $\overline{AB}$, whose distance from $A$ is a quarter of the distance between $A$ and $B$. Find the vector $\overrightarrow{ON}$.

3. Consider the vectors $\mathbf a = \langle 3, 2\rangle$ and $\mathbf b = \langle 2, -1\rangle$.

   a. Draw the vectors: (i) $0.5 \mathbf a + 0.5 \mathbf b$; (ii) $2 \mathbf a - \mathbf b$; and (iii) $1.5 \mathbf a - 0.5 \mathbf b$.

   b. Choose any two scalars $s$ and $t$ that add up to 1. Then, draw the vector $s \mathbf a + t\mathbf b$. (Choose $s$ and $t$ so that the resulting vector is different from any of the vectors in part (a)).

   c.Describe what you observe from parts (a) and (b). That is, describe the vectors obtained by adding $s$ times $\mathbf a$ and $t$ times $\mathbf b$, whenever $s + t = 1$.

   d. Describe the vectors obtained by adding $s$ times $\mathbf a$ and $t$ times $\mathbf b$, whenever $s + t = 1$ and $s$ and $t$ are nonnegative.

4. Find the vectors whose lengths and directions are given: \begin{enumerate}

   a.length = $\frac{1}{\sqrt{14}}$, direction = $-3 \mathbf i + 2 \mathbf j + \vec k$

   b. length = $\frac{13}{12}$, direction = $\frac{3}{13} \mathbf i - \frac{12}{13} \mathbf j + \frac{4}{13} \mathbf k$

5. Compute the scalar triple product $\mathbf u \cdot (\mathbf v \times \mathbf w)$, where $\mathbf u, \mathbf v, \mathbf w$ are as follows: \begin{eqnarray*} \mathbf u & = & 2\mathbf i - 2 \mathbf j + 4\mathbf k\\ \mathbf v & = & 2\mathbf i +9 \mathbf j -\mathbf k \\ \mathbf w & = & 4 \mathbf i + 7 \mathbf j + 3 \mathbf k. \end{eqnarray*} Then, explain how you can tell that all three vectors lie on the same plane from the value of the scalar triple product that you computed above. (Hint: What is $\mathbf u$ perpendicular to?)

6. Suppose that $\mathbf u$ and $\mathbf v$ are nonzero vectors in $\mathbb{R}^3$. Show that the vector $\mathbf u - \operatorname{proj}_{\mathbf v} \mathbf u$ is orthogonal to $\operatorname{proj}_\vec{v}\vec u$.

bonus Use this result to find the point on the plane containing $(0,0,0)$, $(1,1,0)$, and $(0,1,1)$ that is closest to the point $(1,0,0)$.

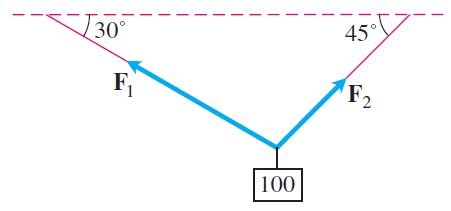
7. Consider a 100 Newton weight suspended by two wires as shown in the figure below. Find the magnitudes and the $\mathbf i$- and $\mathbf j$- components of the force vectors $\mathbf F_1$ and $\mathbf F_2$.