Homework 1

Due: January 22, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1.   a. Let $\mathcal{S}$ be the solid region first octant bounded by the coordinate planes and the planes $x = 3$, $y = 3$, and $z = 4$ (including points on the surface of the region). Sketch, or describe the shape of the solid region $\mathcal{E}$ consisting of all points that are at most 1 unit of distance from some point in $\mathcal{S}$. Also find the volume of $\mathcal{E}$.

   b. Write an equation that describes the set of all points that are equidistant from the origin and the point $(2, -1, -2)$. What does this set look like?

a. The region $\mathcal{E}$ simply extends 1 unit out from each face of the rectangular prism. The interesting part is what happens near the edges and corners. The 12 edges yield 3 cylinders of unit radius and lengths 3, 3, and 4. The 8 corners yield a unit sphere. 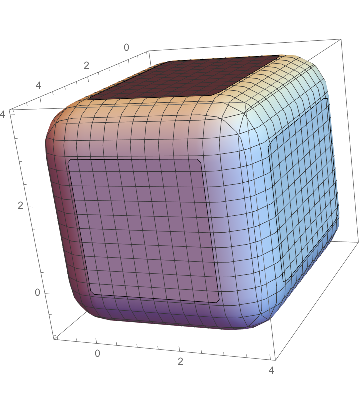Total volume is $$36+2(9)+2(12)+2(12) + 3\pi+3\pi+4\pi+\frac43 \pi = 102+\frac{34}{3}\pi$$

b. A point $(x,y,z)$ is in this region if its distances (squared) to each point are equal. We set up the equation

$$x^2 + y^2 + z^2 = (x-2)^2+(y+1)^2+(z+2)^2$$

We simplify this to the linear equation $$-4x+2y+4z = -9.$$

2. Consider the points $A = (0, -3, -1)$ and $B = (1, 2, -2)$. Let $O$ denote the origin, $(0, 0, 0)$.

   a. Let $M$ denote the midpoint of the line segment $\overline{AB}$. Find the vector $\overrightarrow{OM}$.

   b. Let $N$ denote the point on the line segment $\overline{AB}$, whose distance from $A$ is a quarter of the distance between $A$ and $B$. Find the vector $\overrightarrow{ON}$.

\begin{eqnarray*} \overrightarrow{OM} & = & \overrightarrow{OA} + \frac{1}{2} \overrightarrow{AB} \\ & = & \langle 0, -3, -1 \rangle + \frac{1}{2} \left( \langle 1, 2, -2 \rangle - \langle 0, -3, -1 \rangle\right) \\ & = & \langle 0, -3, -1 \rangle + \langle 0.5, 2.5, -0.5 \rangle \\ & = & \langle 0.5, -0.5, -1.5\rangle. \end{eqnarray*}

\begin{eqnarray*} \overrightarrow{ON} & = & \overrightarrow{OA} + \frac{1}{4} \overrightarrow{AB} \\ & = & \langle 0, -3, -1 \rangle + \frac{1}{4} \left( \langle 1, 2, -2 \rangle - \langle 0, -3, -1 \rangle\right) \\ & = & \langle 0, -3, -1 \rangle + \langle 0.25, 1.25, -0.25 \rangle \\ & = & \langle 0.25, -1.75, -1.25\rangle. \end{eqnarray*}

3. Consider the vectors $\mathbf a = \langle 3, 2\rangle$ and $\mathbf b = \langle 2, -1\rangle$.

   a. Draw the vectors: (i) $0.5 \mathbf a + 0.5 \mathbf b$; (ii) $2 \mathbf a - \mathbf b$; and (iii) $1.5 \mathbf a - 0.5 \mathbf b$.

   b. Choose any two scalars $s$ and $t$ that add up to 1. Then, draw the vector $s \mathbf a + t\mathbf b$. (Choose $s$ and $t$ so that the resulting vector is different from any of the vectors in part (a)).

   c.Describe what you observe from parts (a) and (b). That is, describe the vectors obtained by adding $s$ times $\mathbf a$ and $t$ times $\mathbf b$, whenever $s + t = 1$.

   d. Describe the vectors obtained by adding $s$ times $\mathbf a$ and $t$ times $\mathbf b$, whenever $s + t = 1$ and $s$ and $t$ are nonnegative.

a. b. This becomes much easier when graphed on a single set of axes.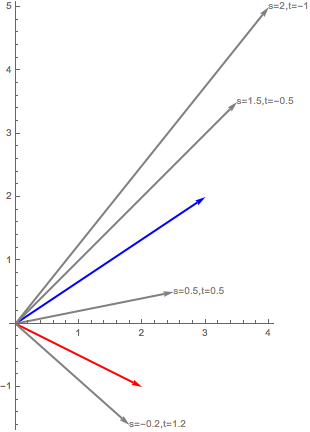

c. This is the set of position vectors along the line connecting the tips of $\vec a$ and $\vec b$.

d. By restricting both to be only positive, then neither is greater than one, so we only get the line segment between the points corresponding to $\vec a$ and $\vec b$.

4. Find the vectors whose lengths and directions are given:

   a.length = $\frac{1}{\sqrt{14}}$, direction = $-3 \mathbf i + 2 \mathbf j + \vec k$

   b. length = $\frac{13}{12}$, direction = $\frac{3}{13} \mathbf i - \frac{12}{13} \mathbf j + \frac{4}{13} \mathbf k$

For general $c\ge 0$, $c\frac{\vec v}{|\vec v|}$ has the same direction as $\vec v$ but length $c$.

a. $ -\frac{3}{14} \mathbf i + \frac{2}{14} \mathbf j + \frac{1}{14}\vec k$

b. $ \frac{3}{12} \mathbf i - \frac{12}{12} \mathbf j + \frac{4}{12} \mathbf k$

5. Compute the scalar triple product $\mathbf u \cdot (\mathbf v \times \mathbf w)$, where $\mathbf u, \mathbf v, \mathbf w$ are as follows: \begin{eqnarray*} \mathbf u & = & 2\mathbf i - 2 \mathbf j + 4\mathbf k\\ \mathbf v & = & 2\mathbf i +9 \mathbf j -\mathbf k \\ \mathbf w & = & 4 \mathbf i + 7 \mathbf j + 3 \mathbf k. \end{eqnarray*} Then, explain how you can tell that all three vectors lie on the same plane from the value of the scalar triple product that you computed above. (Hint: What is $\mathbf u$ perpendicular to?)

$\vec v \times \vec w = 34 \vec i - 10\vec j -22 \vec k$

$\vec u\cdot(\vec v \times \vec w) = 68 + 20 -88 = 0$

So $\vec u$ is perpendicular to the line perpendicular to the plane containing $\vec v and \vec w$ (picture everything with tail at the origin), so it must be in the same plane as $\vec v$ and $\vec w$.

6. Suppose that $\mathbf u$ and $\mathbf v$ are nonzero vectors in $\mathbb{R}^3$. Show that the vector $\mathbf u - \operatorname{proj}_{\mathbf v} \mathbf u$ is orthogonal to $\operatorname{proj}_\vec{v}\vec u$.

bonus Use this result to find the point on the plane containing $(0,0,0)$, $(1,1,0)$, and $(0,1,1)$ that is closest to the point $(1,0,0)$.

$\operatorname{proj}_\vec v \vec u$ is a scalar multiple of $\vec v$, so it suffices to show

\begin{align*} (\vec u - \operatorname{proj}_\vec v \vec u)\cdot\vec v &= (\vec u - \frac{\vec u \cdot \vec v}{\vec v \cdot \vec v}{\vec v})\cdot \vec v \\ \ & = \vec u \cdot \vec v - \frac{\vec u \cdot \vec v}{\vec v \cdot \vec v}{\vec v\cdot \vec v} \\ \ & = \vec u \cdot \vec v - \vec u \cdot \vec v \\ \ & = 0. \end{align*}

bonus $$\frac23\vec i + \frac13\vec j -\frac13\vec k $$

7. Consider a 100 Newton weight suspended by two wires as shown in the figure below. Find the magnitudes and the $\mathbf i$- and $\mathbf j$- components of the force vectors $\mathbf F_1$ and $\mathbf F_2$.

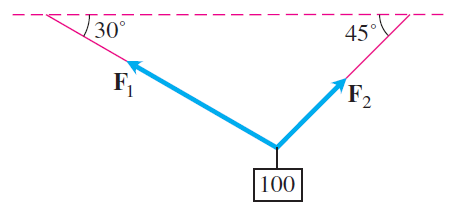
Let $\vec W = 0 \vec i - 100 \vec j$ denote the downward-pointing vector due to the weight.

Since the hanging mass is not moving, it must be the case that the sum of all three vectors is zero: $$ \vec F_1 + \vec F_2 + \vec W = 0 \vec i + 0 \vec j.$$ That is, $$ (-a\sqrt{3}/2 \ \vec i + a \sqrt{3}/2 \ \vec j) + (b\sqrt{2}/2 \ \vec i + b \sqrt{2}/2 \ \vec j) + (0 \vec i - 100 \vec j) = 0 \vec i + 0 \vec j. $$ Separating this into two equations, one for the $\vec i$ component and one for the $\vec j$ component: \begin{eqnarray*} -a\sqrt{3}/2 + b\sqrt{2}/2 + 0& = & 0 \\ a/2 + b \sqrt{2}/2 - 100 & = & 0 \end{eqnarray*} Since there are two equations and two unknowns, we can solve for $a$ and for $b$. For example, we can eliminate $b$ by subtracting the second equation from the first equation to obtain: $$ -a (\sqrt{3}/2 + 1/2) + 100 = 0 $$ $$ a = \frac{200}{1+\sqrt{3}}.$$ Using the first equation to solve for $b$: $$ a\sqrt{3}/2 = b \sqrt{2}/2$$ $$ b = \frac{200}{1 + \sqrt{3}} \ \frac{\sqrt{3}}{\sqrt{2}} = \frac{100\sqrt{6}}{1 + \sqrt{3}}. $$ So, the magnitudes of the vectors: $|\vec F_1 | = \frac{200}{1+\sqrt{3}} \approx 73.21 \text{ N}$ and $|\vec F_2 | = \frac{100\sqrt{6}}{1 + \sqrt{3}} \approx 89.66\text{ N}$.

Therefore, the components of the vectors are: $$\vec F_1 = -\frac{100\sqrt{3}}{1 + \sqrt{3}} \vec i + \frac{100}{1 + \sqrt{3}} \vec j, ~~ \vec F_2 = \frac{100\sqrt{3}}{1 + \sqrt{3}} \vec i + \frac{100\sqrt{3}}{1 + \sqrt{3}} \vec j.$$