Homework 10 Solutions

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. Each vctor field below has the form $\vec F(x,y) = P(x,y)\,\vec i + Q(x,y)\,\vec j$ where $P$ and $Q$ are sepelcted from among the functions $$\{\pm x,\pm y,\pm x^2,\pm y^2,\pm \cos(x),\pm \cos y \}.$$

For each, find $P$ and $Q$ and briefly describe how you arrived at your conclusion.

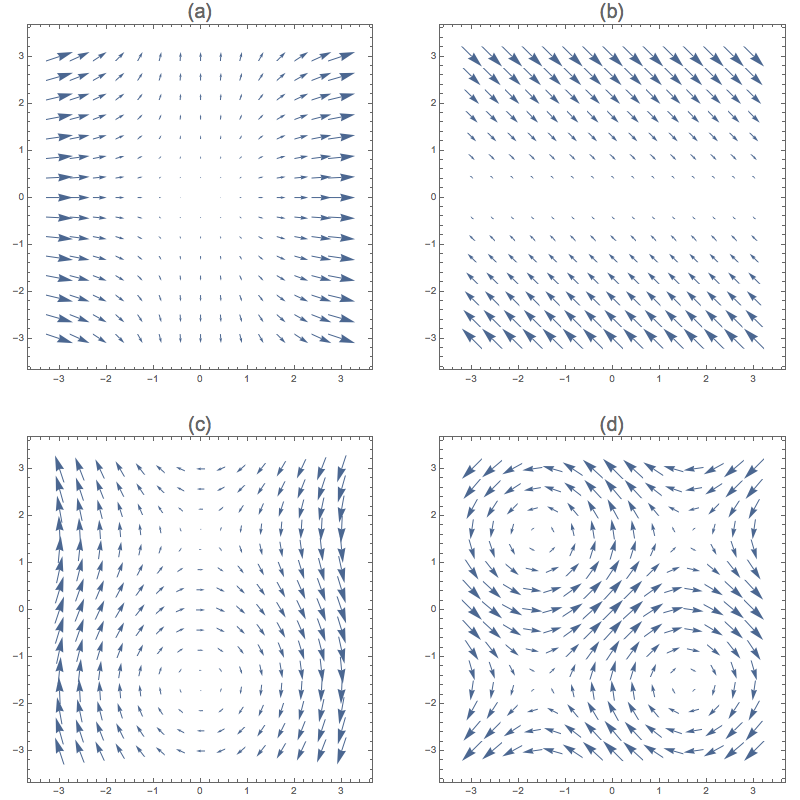
a. $x^2\,\vec i + y\,\vec j$. $P$ is always positive and independent of $y$. $Q$ is positive when $y$ is positive and negative when it is negative.

b. $y\,\vec i - y\,\vec j$. Independent of $x$ overall. Signs determine the rest.

c. $\cos y\,\vec i - x\,\vec j$ The $\vec i$-component is poitive near the %x%-access and flips sign around $\pm\frac32$ (actually $\pi/2$). The $\vec j$-component varies with the opposite sign of $x$. d. $\cos y\,\vec i +\cos x \,\vec j$. Check $y=0$ to see oscillation in $\vec j$-component, and $x=0$ to see oscillation in $\vec i$ component.

2. Determine a potential function $f(x,y,z)$ for the following conservative vector field.

$$ \vec F(x,y,z) = \left(\frac{1}{x}+y z^2-3\right)\,\vec i+\left(x z^2-z \sin (y z)\right)\,\vec j +\left(2 x y z-y \sin (y z)+\frac{1}{z}\right)\,\vec k $$

From the3 first component, $$f(x,y,z) = \int \left(\frac{1}{x}+y z^2-3\right)dx = \ln |x| + xyz^2 -3x +g(y,z)$$

Differentiate with repect to $y$ and set equal to second component.

$$f_y(x,y,z) = xz^2+g_y(y,z) = x z^2-z \sin (y z)$$

Thus, $$g(y,z) = \int -z \sin (yz) dy = \cos (yz) +h(z)$$.

Then check the last component.

$$f_z(x,y,z) = 2xyz -y\sin(yz) +h'(z) = 2 x y z-y \sin (y z)+\frac{1}{z}$$

Thus, $h(z) = \ln|z| + C$. Finally,

$$f(x,y,z) = xyz^2 -3x + \cos (yz) +\ln |xz| + C$$

3. Compute the line integral $ \int_C f \,ds$ (i.e., with respect to arclength) where the curve $C$ is graphed below (oriented counterclockwise) and $$f(x,y) = x^2 + y^2. $$

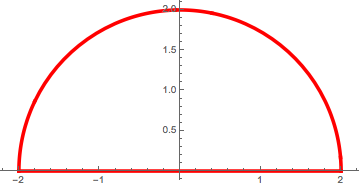
(You may use the interpretation $\int_C f\,ds$ given in class and/or use the formula $$\int_c f\,ds = \int_a^b f(\vec r(t)) |\vec r'(t)|\,dt $$ as explained in §16.2 of the text.)

We do the integral in two pieces. First, the arc can be parametrized with $\vec r(t) = 2\cos t\,\vec i + 2 \sin t\,\vec j$ for $0 \leq t \leq \pi$. Thus $|\vec r'(t)| = 2$. So we integrate $$\int_0^\pi \left(4\cos^2 t+4sin^2 t\right)2dt = 8\pi.$$

Next, the bottom part can be parametrized simply by $\vec q (t) = t\,\vec i$ for $-2\leq t \leq 2$, and thus $|\vec q'(t)| = |\vec i|=1$. Thus,

$$\int_{-2}^2 t^2dt = \frac{16}{3}$$

and the whole line integral is $8\pi + \frac{16}{3}$.