Homework 11

Due: April 10, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

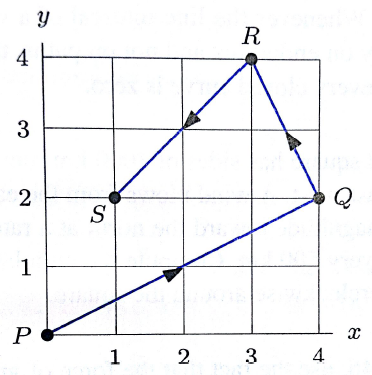
1. Compute $\int_C \vec F \cdot d\vec r$, where $C$ is the oriented curve in the figure, and $\vec F$ is the vector field that is constant on each of the three straight segments of $C$: $$ \vec F(x, y) = \left \{ \begin{array}{l c l} x\,\vec i & & \text{on } PQ \\ 2x\,\vec i - \vec j & & \text{on } QR \\ 3x\,\vec i + \vec j & & \text{on } RS. \end{array}\right.$$

2. Suppose $g:\R\to\R$ is a smooth, nonconstant function.

• Show that $g(x)\,\vec i$ is a conservative vector field.
• Then, use the idea of path-independence (i.e., use Theorem 4 from §16.3) to show $g(x)\,\vec j$ is not conservative. (Hint: construct two paths with common endpoints but different line integrals of the vector field.)

3. Let $\vec F = 3x^2 y^2\,\vec i + 2x^3 y\,\vec j$ and let $C$ be the path in the $xy$-plane from $(-1, 1)$ to $(1, 1)$ that consists of the line segment from $(-1, 1)$ to $(0, 0)$ followed by the line segment from $(0, 0)$ to $(1, 1)$. Evaluate $\displaystyle\int_C \vec F \cdot d\vec r$ in two ways:

  a. Find parametrizations for the segments that make up $C$, and evaluate $\displaystyle\int_C \vec F \cdot d\vec r$.

  b.Find a potential function $f$ for $\vec F$ and use it to to evaluate $\displaystyle\int_C \vec F \cdot d\vec r$.

4. Find a value $c$ such that the work done by a force field $$ \vec F (x,y) = \langle 4-x^2y,-xy \rangle $$ on an object moving along the parabolic path $y=c(1-x^2)$ from $(-1,0)$ to $(1,0)$ is a minimum. Compare the result with the straight line segment ($c = 0$) running between the two points.

5. Use Green's theorem to evaluate each line integral below or explain how it does not apply.

• $$\displaystyle\int_C \frac{1}{\sqrt{x^2 + y^2}} \ dx - \frac{1}{\sqrt{x^2 + y^2}} \ dy$$ where $C$ is the unit circle centered at the origin, oriented counterclockwise.

• $$\displaystyle\int_C (x^2 + y^2) dx + (x^2 + y^2 ) \ dy$$ where $C$ is the boundary of the region bounded by $y = x$, $y = x^2$, $0 \leq x \leq 1$, with counterclockwise orientation.

• $\displaystyle\int_C \vec F \cdot d\vec r$ where $\vec F = x \vec i + y \vec j$ and $C$ is the line segment from the origin to the point $(1,1)$.

6.

  a. Show that for the vector field $\vec F(x,y) = \frac12 \langle -y,x$, the line integral $\oint \vec F\cdot d\vec r$ over a simple, closed curve $C$ is the area enclosed by $C$.

  b. Use part (a) to compute the area enclosed by one "leaf" of the trefoil given in polar coordinates by $r=\sin(3\theta)$ for $0\le \theta \le \pi$.

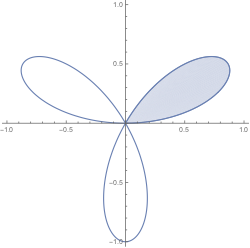
(You must first parametrize this curve. The integrand looks awful at one point but simplifies greatly.)