Homework 11 Solution

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

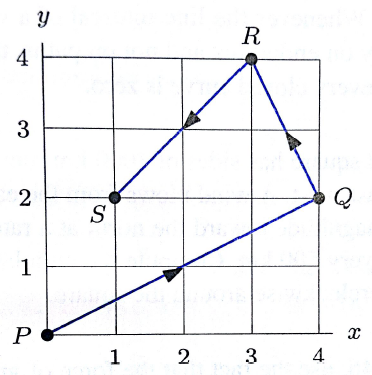
1. Compute $\int_C \vec F \cdot d\vec r$, where $C$ is the oriented curve in the figure, and $\vec F$ is the vector field that is constant on each of the three straight segments of $C$: $$ \vec F(x, y) = \left \{ \begin{array}{l c l} x\,\vec i & & \text{on } PQ \\ 2x\,\vec i - \vec j & & \text{on } QR \\ 3x\,\vec i + \vec j & & \text{on } RS. \end{array}\right.$$

Solution

First, we can parametrize each segment with $0\leq t \leq 1$ (but there are many choices here). \begin{align*} \vec r_1(t) &= 4t\,\vec i + 2t\,\vec j \\ \vec r_2(t) &= (4-t)\,\vec i + (2+2t)\,\vec j \\ \vec r_3(t) &= (3-2t)\,\vec i + (4-2t)\,\vec j \end{align*} Then plug into $\int_C \vec F\cdot d \vec r = \int_a^b \vec F(\vec r(t))\cdot \vec r'(t)\,dt$.

\begin{align*} & \int_0^1 4t (4) dt \\ & + \int_0^1 2(4-t)(-1) + (-1) (2)\,dt \\ & + \int_0^1 3(3-2t)(-2) + (-2)\,dt \\ & = 8-9-14=-15 \end{align*}

2. Suppose $g:\R\to\R$ is a smooth, nonconstant function.

• Show that $g(x)\,\vec i$ is a conservative vector field.

Solution

Let $G(x)$ be an antiderivative of $g$ (every continuous function has one). Then taken as a multivariable function, $G$ has only one nonzero partial derivative, so $\nabla G = g(x)\,\vec i$. Thus, the vector field is conservative.

• Then, use the idea of path-independence (i.e., use Theorem 4 from §16.3) to show $g(x)\,\vec j$ is not conservative. (Hint: construct two paths with common endpoints but different line integrals of the vector field.)

Solution

Since $g$ is noncenstant we can find $g(a)\neq g(b)$. Now consider 2 paths:

• Let $C_1$ be the polygonal path from $(a,0)$ to $(a,1)$ to $(b,1)$.
• Let $C_2$ be the polygonal path from $(a,0)$ to $(b,0)$ to $(b,1)$.

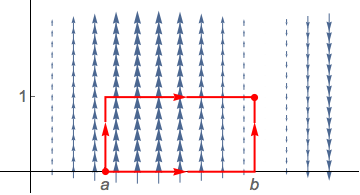
The "horizontal" sections of each path are orthogonal to the vector field and so the line integral yields 0 there. The "vertical" sections have parametrizations $a\,\vec i + t\,\vec j$ and $b\,\vec i + t\,\vec j$, respectively. Each has tangent vector $\vec j$. Ans so we compute \begin{align*} \int_{C_1} \langle 0,g(x)\rangle \cdot d\vec r &= \int_0^1 \langle 0,g(a)\rangle\cdot\langle 0,1\rangle \,dt =\int_0^1 g(a)\,dt = g(a) \\ \int_{C_2} \langle 0,g(x)\rangle \cdot d\vec r &= \int_0^1 \langle 0,g(b)\rangle\cdot\langle 0,1\rangle \,dt =\int_0^1 g(b)\,dt = g(b) \end{align*} which are, by assumption, differnt. Thus the vector field is not path-independent and hence, not coservative.

3. Let $\vec F = 3x^2 y^2\,\vec i + 2x^3 y\,\vec j$ and let $C$ be the path in the $xy$-plane from $(-1, 1)$ to $(1, 1)$ that consists of the line segment from $(-1, 1)$ to $(0, 0)$ followed by the line segment from $(0, 0)$ to $(1, 1)$. Evaluate $\displaystyle\int_C \vec F \cdot d\vec r$ in two ways:

  a. Find parametrizations for the segments that make up $C$, and evaluate $\displaystyle\int_C \vec F \cdot d\vec r$.

  b. Find a potential function $f$ for $\vec F$ and use it to to evaluate $\displaystyle\int_C \vec F \cdot d\vec r$.

Solution

a. $\vec r(t) = t\,\vec i + |t|\,\vec j$ accomplishes this for $-1\leq t \leq 1$ but since this is piecewise defines, we have to split the computation into two integrals anyway. $$ \int_{-1}^0 (3t^2(-t)^2\,\vec i + 2t^3(-t)\,\vec j)\cdot (\vec i - \vec j)\,dt + \int_{0}^1 (3t^4\,\vec i + 2t^4\,\vec j)\cdot (\vec i + \vec j)\,dt $$ $$ = \int_{-1}^1 5t^4\,dt = t^5\mid_{-1}^1 = 2 $$

b. We solve $\nabla f = \vec F$: \begin{align*} f_x &= 3x^2 \\ f_y &= 2x^3y \end{align*} So $f(x,y) = x^3y^2 + g(y)$ for some differentiable function $g$. By second equation, we see $g(y)$ is a constant. Might as well pick 0. Applying the FTLI, we get $$ \int_C \vec F \cdot d\vec r = f(1,1) - f(-1,1) = 1 - (-1) = 2 $$

4. Find a value $c$ such that the work done by a force field $$ \vec F (x,y) = \langle 4-x^2y,-xy \rangle $$ on an object moving along the parabolic path $y=c(1-x^2)$ from $(-1,0)$ to $(1,0)$ is a minimum. Compare the result with the straight line segment ($c = 0$) running between the two points.

Solution

Here is the curve graphed for several values of $c$.

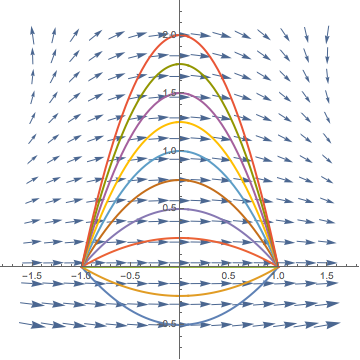
We can parametrize the curve, the graph of a function, with \begin{align*} \vec{r}(t) &= \langle t, c(1-t^2)\rangle \\ \vec{r}'(t) &= \langle 1,-2ct \rangle \\ -1 &\leq t \leq 1 \end{align*}

We write the work done as a function of $c$. \begin{align*} W(c) &= \int_{C_c} \vec{f}\dot d\vec{r} = \int_{-1}^1\langle 4- t^2 c(1-t^2),-t c (1-t^2) \rangle\dot\langle1,-2 c t \rangle\,dt \\ &= \int_{-1}^1 (-2 c^2 t^4+2 c^2 t^2+c t^4-c t^2+4)\,dt \\ &= \frac{8 c^2}{15}-\frac{4 c}{15}+8 \end{align*}

This function is a concave-up quadratic function which thus has a minimum where $W'(c) = \frac{16}{15}c-\frac{4}{15} = 0$, or at $c=\frac14$.

5. Use Green's theorem to evaluate each line integral below or explain how it does not apply.

• $$\displaystyle\int_C \frac{1}{\sqrt{x^2 + y^2}} \ dx - \frac{1}{\sqrt{x^2 + y^2}} \ dy$$ where $C$ is the unit circle centered at the origin, oriented counterclockwise.

• $$\displaystyle\int_C (x^2 + y^2) dx + (x^2 + y^2 ) \ dy$$ where $C$ is the boundary of the region bounded by $y = x$, $y = x^2$, $0 \leq x \leq 1$, with counterclockwise orientation.

• $\displaystyle\int_C \vec F \cdot d\vec r$ where $\vec F = x \vec i + y \vec j$ and $C$ is the line segment from the origin to the point $(1,1)$.

Solution

• We can use Green's Theorem for I since $D$ is a simple closed curve that is piecewise smooth (and positively-oriented), and $P$ and $Q$ have continuous partial derivatives (everywhere on $\R^2$).

Let $D$ denote the region bounded by $C$. Then, using Green's Theorem, \begin{eqnarray*} \int_C (x^2 + y^2) \ dx + (x^2 + y^2) \ dy & = & \iint_D 2x - 2y \ dA \\ & = & \int_{0}^1 \int_{x^2}^x 2x - 2y \ dy \ dx \\ & = & \int_{0}^1 \left.2xy\right|_{x^2}^x - \left.y^2\right|_{x^2}^x \ dx \\ & = & \int_0^1 2x^2 - 2x^3 - x^2 + x^4 \ dx \\ & = & \frac{1}{30} \end{eqnarray*}

• We cannot use Green's Theorem for II since $P$ and $Q$ (and their partial derivatives) are not continuous at $(0, 0)$, which is inside the region bounded by $C$.

• We cannot use Green's Theorem for III directly since $C$ is not a closed curve.

6.

  a. Show that for the vector field $\vec F(x,y) = \frac12 \langle -y,x$, the line integral $\oint \vec F\cdot d\vec r$ over a simple, closed curve $C$ is the area enclosed by $C$.

Solution

By Green's Theorem, we know $$ \oint_C \vec F\cdot d\vec r = \oint_C P\,dx + Q\,dy = \iint_D Q_x-P_y\,dA. $$ where $P(x,y) = -\frac12y $ and $Q(x,y) = \frac12x$ so the integrand on the RHS is $Q_x-P_y = \frac12 - -\frac12 = 1$ and the integral of 1 over a region gives area.

  b. Use part (a) to compute the area enclosed by one "leaf" of the trefoil given in polar coordinates by $r=\sin(3\theta)$ for $0\leq \theta \leq \pi$.

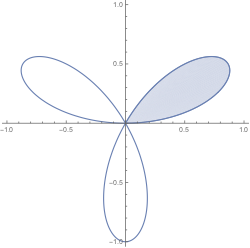
Solution

This is a polar curve of the form $r=f(\theta)$ for $\theta_1 \leq \theta \leq \theta_2$. These can always be parametrized by using polar coordinates and converting to rectangular:

\begin{align*} x & = r \cos \theta = f(\theta)\cos\theta \\ y & = r \sin \theta = f(\theta)\sin \theta \end{align*}

This gives $x$ and $y$ as functions of a single variable $\theta$. That is what a parametrized curve is. More specifically here (and changing $\theta$ to $t$ to save keystrokes):

The curve is parametrized by $$ \vec r(t) = \langle x(t),y(t)\rangle = \langle \sin(3t)\cos(t),\sin(3t)\sin(t)\rangle $$ where $0\leq t\leq \frac\pi3$.

Thus we compute \begin{align*} \oint_C \vec F\cdot d\vec r &= \frac12\oint_C-y\,dx + x\,dy \\ &= \frac12\int_0^{\pi/3} -\sin(3t)\sin(t)\left( 3\cos (3t)\cos t-\sin(3t)\sin(t) \right) dt \\ & ~~~~~+ \frac12\int_0^{\pi/3} \sin(3t)\cos(t) \left( 3\cos (3t)\sin t+\sin(3t)\cos(t) \right) dt \\ &= \frac12\int_0^{\pi/3} \sin^2(3t)\,dt \\ &= \frac12\int_0^{\pi/3} \frac{1-\cos(6t)}{2} ,dt \\ &= \frac{\pi}{12} \end{align*}