Homework 12¶
Due: April 17, 2018, 8 a.m.¶
Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.
Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.
$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$
1. For each of the following vector fields, determine if the divergence is positive, zero, or negative at the indicated point. Explain/justify your answer.
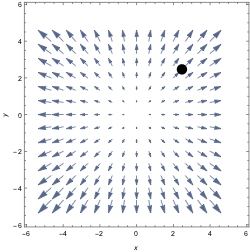
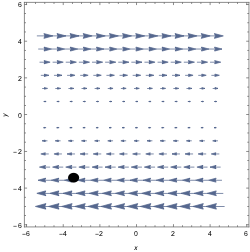
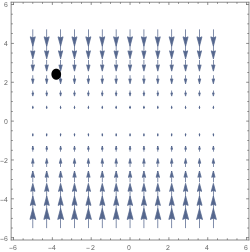
2. Let $f$ be a smooth, scalar-valued function on $\R^3$ and let $\vec F$ be a smooth vector field on $\R^3$. For each expression below:
i. Determine if at a given point $(x,y,z)$, it is a scalar, a vector, or invalid.
ii. If invalid, explain.
iii. If valid, prove that the expression is identically $0$ or $\vec 0$, or give a specific counterexample.
- $\displaystyle \nabla\times\nabla f$
- $\displaystyle \nabla(\nabla\times F)$
- $\displaystyle \nabla\cdot(\nabla\times F)$
- $\displaystyle \nabla\cdot\nabla f$
3. A torus of revolution (doughnut) is obtained by rotating a circle $C$ in the $xz$ plane about the $z$-axis. Suppose that $C$ has a radius $r$ and center $(R, 0, 0)$. Here, $R>r$.
- Find a parametrization $\vec r(u, v)$ of the torus. Specify the set $D$ in which $(u, v)$ must lie.
Hint: You can choose to let $u$ represent the angle that the line from the point $\vec r(u, v)$ on the torus to the center of the rotated circle form with the $xy$-plane, and let $v$ denote the angle formed by the line from the point $\vec r(u, v)$ on the torus to the origin with the positive $x$-axis. See figures below.
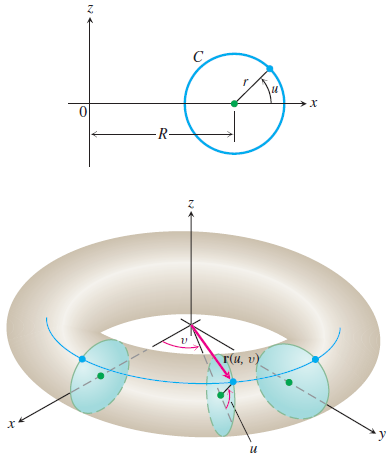
- Show that the surface area of the torus is $4\pi^2Rr$.
4. Find a parametrization of the portion of the paraboloid $z = \frac{x^2 + y^2}{4}$ between the planes $z = 1$ and $z = 2.25$. Use the parametrization to formulate the area of the surface as a double integral. Then, evaluate the integral.
5. Suppose an hourglass (as pictured) is 15 cm tall, 8 cm across at its widest and .25 cm across at the narrow part. Find a reasonable parametrization for the (outside) surface of the glass and use it to compute its surface area.
