Homework 12 Solution

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\pa}{\partial} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. For each of the following vector fields, determine if the divergence is positive, zero, or negative at the indicated point. Explain/justify your answer.

Solution\

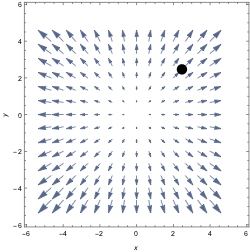
As $x$ increases, the horizontal component of the vector field is increasing (more positive). Ditto for the vertical component in the $y$-direction. The sum of two positive quantities is positive.

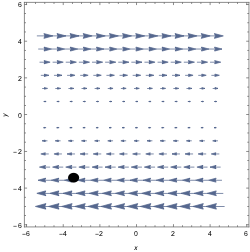
The horizontal component is not changing as $x$ changes, so $P_x=0$. $Q=0$ everywhere, so of course $Q_y =0$. This field has divergence 0.

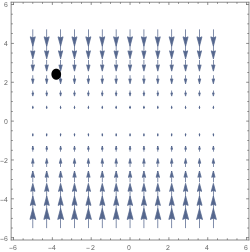
The horizontal component is 0 everywhere. At the point labeled, the vertical component is decreasing (getting more negative) as $y$ increases. Thus $P_x + Q_y = 0 +Q_y < 0$.

2. Let $f$ be a smooth, scalar-valued function on $\R^3$ and let $\vec F$ be a smooth vector field on $\R^3$. For each expression below:

i. Determine if at a given point $(x,y,z)$, it is a scalar, a vector, or invalid.

ii. If invalid, explain.

iii. If valid, prove that the expression is identically $0$ or $\vec 0$, or give a specific counterexample.

Solution

• $\displaystyle \nabla\times\nabla f$

The curl of the gradient of a scalar field is a vector field. Further, $$\nabla \times\nabla f = \begin{vmatrix} \vec i & \vec j & \vec k \\ \pa_x & \pa_y & \pa_z \\ f_x & f_y & f_z \end{vmatrix} = (f_{zy}-f_{yz})\vec i + (f_{xz}-f_{zx})\vec j + (f_{yx}-f_{xy})\vec k = \vec 0$$

• $\displaystyle \nabla(\nabla\times F)$

Invalid. Cannot take the gradient of a vector field.

• $\displaystyle \nabla\cdot(\nabla\times F)$

Divergence of a curl is a scalar field. In fact, it is identically 0.

$$\nabla\cdot(\nabla \times \vec F) = \pa_x(R_y-Q_z) + \pa_y(P_z - R_x) + \pa_z(Q_x-P_y) = R_{yx}-R_{xy} -Q_{zy} + Q_{yz} +P_{zy} - P_{yz} = 0$$

• $\displaystyle \nabla\cdot\nabla f$

The divergence of the gradient (aka the Laplacian) of a scalar field is a scalar field.

$$\nabla\cdot\nabla f = f_{xx}+f_{yy}+f_{zz} $$

This is not necessarily 0. Take, for example, $f(x,y) = x^2 + y^2$. Then $$f_{xx} + f_{yy} = 2 +2 = 4.$$

3. A torus of revolution (doughnut) is obtained by rotating a circle $C$ in the $xz$ plane about the $z$-axis. Suppose that $C$ has a radius $r$ and center $(R, 0, 0)$. Here, $R>r$.

• Find a parametrization $\vec r(u, v)$ of the torus. Specify the set $D$ in which $(u, v)$ must lie.

Hint: You can choose to let $u$ represent the angle that the line from the point $\vec r(u, v)$ on the torus to the center of the rotated circle form with the $xy$-plane, and let $v$ denote the angle formed by the line from the point $\vec r(u, v)$ on the torus to the origin with the positive $x$-axis. See figures below.

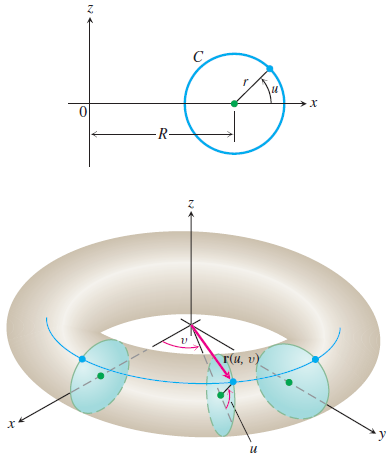
• Show that the surface area of the torus is $4\pi^2Rr$.

Solution

First, consider the circle $C$ in the $xz$-plane: $y = 0$ and $(x-R)^2 + z^2 = r^2$.

$x-R = r \cos u$ and $z = r\sin u$, where $u \in [0, 2\pi]$. Then, the parametric equations for $(x, z)$ on $C$ is: \[ x = R + r\cos u, ~~ z = r\sin u, ~ u \in [0, 2\pi]. \] We revolve the circle about the $z$-axis. Hence, \[ x = (R + r\cos u ) \cos v, ~~ y = (R+r \cos u) \sin v, ~~ z = r \sin u, ~ u \in [0,2\pi], ~v \in [0, 2\pi]. \] We can also write this as: \[ \vec r(u, v) = (R + r\cos u ) \cos v \ \vec i + (R + r\cos u ) \sin v \ \vec j + r \sin u \ \vec k,\] \[ (u, v) \in D = [0, 2\pi] \times [0, 2\pi]. \]

We find $|\vec r_u \times \vec r_v|$: \begin{eqnarray} \vec r_u(u, v) & = & \langle -r \sin u \cos v, -r\sin u \sin v, r\cos u \rangle, \ \vec r_v(u, v) & = & \langle -(R + r\cos u) \sin v, (R + r\cos u) \cos v, 0 \rangle,\ \vec r_u \times \vec r_v & = & \langle -r(R+r\cos u) \cos u \cos v, -r(R+r\cos u) \cos u \sin v, -r(R+r\cos u) \sin u\rangle. \end{eqnarray} Therefore, \[ |\vec r_u \times \vec r_v| = r (R + r\cos u). \]

Then, the surface area of the torus is \begin{eqnarray} \iint_D |\vec r_u \times \vec r_v| \,dA & = & \int0^{2\pi} \int{0}^{2\pi} r (R + r\cos u) \ du \ dv \ & = & \int_0^{2\pi} 2 \pi Rr + r^2\sin(2\pi) - r^2\sin(0) \ dv \ & = & 2\pi r R (2\pi) = 4 \pi^2Rr, \end{eqnarray} as desired.

4. Find a parametrization of the portion of the paraboloid $z = \frac{x^2 + y^2}{4}$ between the planes $z = 1$ and $z = 2.25$. Use the parametrization to formulate the area of the surface as a double integral. Then, evaluate the integral.

Solution

This is clearly just the graph of a fiunction of $x$ and $y$, but we can express the bounds in $u$ and $v$ most easily using polar coordinates. \[ \begin{bmatrix} x \ y \ z \end{bmatrix} = \begin{bmatrix} x \ y \ f(x,y) \end{bmatrix} = \begin{bmatrix} u \cos v \ u \sin v \ f(u \cos v,y\sin v) \end{bmatrix} = \begin{bmatrix} u \cos v \ u \sin v \ \frac{u^2}{4} \end{bmatrix} \]

Solving the last component for the cutoff planes gives

\[ 2 \leq u \leq 3, ~~~ 0 \leq v \leq 2\pi \]

From there, it's plug-and-chug. \[ \vec r_u \times \vec r_v = \begin{vmatrix}\vec i & \vec j & \vec k \ \cos v & \sin v & u/2 \ -u \sin v & u \cos v & 0 \end{vmatrix} = -\frac{u^2}{2}\cos v\,\vec i - \frac{u^2}{2}\sin v\,\vec j + u\,\vec k\]

Thus the surface area is \[ \iint_D |\vec r_u\times\vec r_v|\,dA = \int_0^{2\pi} \int_2^3 u\sqrt{\frac{u^2}{4}+1}\,du\,dv\]

Substitute $w=u^2/4 + 1, ~ dw = u/2\,du$ to get \[\int_0^{2\pi} \int_2^{13/4} 2 \sqrt{w} \,dw\,dv = \frac{8\pi}{3}(\frac{13^{3/2}}{8}-2^{3/2}) \approx 25.39. \]

5. Suppose an hourglass (as pictured) is 15 cm tall, 8 cm across at its widest and .25 cm across at the narrow part. Find a reasonable parametrization for the (outside) surface of the glass and use it to compute its surface area.

"Solution"

I tried to fit the profile of this object by using a function $f(z)$ as the radius of revolution around the $z$-axis. The parametrization was thus

\[ \begin{bmatrix} x \ y \ z \end{bmatrix} = \begin{bmatrix} f(u) \cos v \ f(u) \sin v \ u \end{bmatrix} \] for $-7.5 \leq u \leq 7.5, 0 \leq v \leq 2\pi$.

This leads to a surface area integral $$\int_0^{2\pi}\int_{-7.5}^{7.5} f(u)\sqrt{1+(f'(u))^2}\,du\,dv $$

I didn't have a lot of luck making this look good. I tried fitting a cubic. 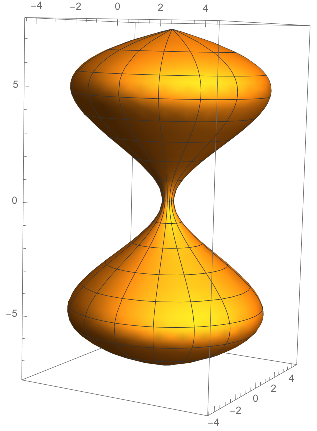which gave a surface area of 362.6 cm$^2$.

And here is a radius-$7.5$ circle with a Gaussian carved out of it.

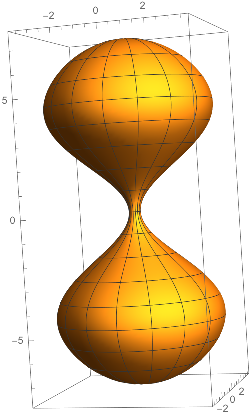
This area was 292 cm$^2$. I hope someone came up with a better looking one.