Homework 13 Solution¶
$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\div}{\operatorname{div}} \newcommand{\curl}{\operatorname{curl}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$
1. Integrate $g(x, y, z) = x\sqrt{y^2+4}$ over the surface $S$ that is the portion of the surface $y^2 + 4z = 16$ that lies between the planes $x = 0$, $x = 1$, and $z = 0$.
Solution¶
Parametrize $S$ by $$\vec r(x,y) = \left\langle x,y, 4-\frac{1}{4}y^2\right\rangle $$ where $0 \leq x \leq 1$ and $-4\leq y \leq 4$. Then \begin{align*} \int_S g \ dS&= \int_{-4}^{4} \int_0^1 g(\vec r(x,y))\, | \vec r_x \times \vec r_y |\, dx\, dy \\ &= \int_{-4}^{4} \int_0^1 x\sqrt{y^2 + 4}\sqrt{1+\frac{1}{4}y^2} \,dx\,dy \\ &= \frac{1}{2} \int_{-4}^{4} \int_0^1 x(y^2 +4)\, dx\,dy \\ &= \frac{56}{3} \end{align*}
2. Find the outward flux of the field $\vec F = xz\, \vec i + yz \,\vec j + \vec k$ across the surface of the portion of the sphere $x^2 + y^2 + z^2 = 25$ above the plane $z = 3$.
Solution¶
Spherical¶
We first parametrize the surface $S$: $$ \vec r(\phi,\theta) = 5\sin \phi\cos\theta \vec i + 5\sin\phi\sin\theta \vec j + 5\cos\phi \vec k, $$ where $0 \le\theta\le 2\pi$ and $\phi \le \cos^{-1}\frac35$
Hence, \begin{align*} \vec r_\phi & = \langle 5\cos\phi\cos\theta,5\cos\phi\sin\theta,-5\sin\phi \rangle\\ \vec r_\theta & = \langle -5\sin\phi\sin\theta , 5\sin\phi\cos\theta,0\rangle\\ \vec r_\phi \times \vec r_\theta & = \langle 5\sin\phi\,5\sin \phi\cos\theta , 5\sin\phi\,5\sin\phi\sin\theta , 5\sin\phi\,5\cos\phi \rangle \\ & = 5\sin\phi \, \vec r. \end{align*}
(This is awful. CAS it.)
\begin{align*} \iint_S \vec F \cdot (\vec r_\phi \times \vec r_\theta) \ dS &= \int_{0}^{2\pi} \int_{0}^{\cos^{-1}(3/5)} 625 \sin ^3(\phi ) \cos (\phi )+25 \sin (\phi ) \cos (\phi ) \ d\phi \ d\theta \\ & = 72 (2\pi) = 144 \pi. \end{align*}
Rectangular¶
We first parametrize the surface $S$: $$ \vec r(x, y) = x \vec i + y \vec j + \sqrt{25-x^2 - y^2} \vec k, $$ where $(x, y) \in D = \{ (x, y) ~|~ x^2 + y^2 \leq 16 \}$ (since we want $z \geq 3$, then $ x^2 + y^2 \leq 25 - 9$).
Hence, \begin{eqnarray*} \vec r_x & = & \left\langle 1, 0, -\frac{x}{\sqrt{25-x^2 - y^2}} \right\rangle\\ \vec r_y & = & \left\langle 0, 1, -\frac{y}{\sqrt{25-x^2 - y^2}} \right\rangle\\ \vec r_x \times \vec r_y & = & \left\langle \frac{x}{\sqrt{25-x^2 - y^2}}, \frac{y}{\sqrt{25-x^2 - y^2}}, 1\right\rangle. \end{eqnarray*} Therefore, $$\vec F \cdot (\vec r_x \times \vec r_y) = x^2 + y^2 + 1, $$ and \begin{eqnarray*} \iint_S \vec F \cdot (\vec r_x \times \vec r_y) \ dS & = & \iint_D x^2 + y^2 + 1 \ dA \\ & = & \int_{0}^{2\pi} \int_{0}^4 (r^2 + 1) r \ dr \ d\theta \\ & = & 72 (2\pi) = 144 \pi. \end{eqnarray*}
3. Let $\vec n$ be the outer unit normal of the surface $S$ given by $4x^2 + 9y^2 + 36z^2 = 26, z \geq 0$, and let $\vec F(x, y, z) = y\vec i + x^2 \vec j + (x^2 + y^4)^{3/2} \sin(e^{\sqrt{xyz}})\vec k$.
Find the value of $$ \iint_S \curl \vec F \cdot d \vec S. $$
Hint: One parametrization of the ellipse at the base of the shell is of the form $x = a \cos(t), y = b\cos(t)$, for some constants $a, b$.
Further Hint: That last compnent of $\vec F$ is so complicated, it must not matter. Why not?
Solution¶
For $ z = 0$ the curve $4x^2 + 9y^2 = 26$ is parametrized by $$ (x,y) \mapsto \bigg( \frac{\sqrt{26}}{2}\cos\theta, \frac{\sqrt{26}}{3}\sin\theta, 0 \bigg) $$ Thus we have \begin{align*} \iint_s \curl \vec F \cdot d\vec s &= \int_c \vec F \cdot d \vec r \\ &= \int_{0}^{2\pi} \bigg(\frac{\sqrt{26}}{3}\sin\theta, \frac{26}{4}\cos^2 \theta, \text{ (who cares?) } \bigg) \\ &\text{ } \hspace{0.35in} \cdot \bigg(-\frac{\sqrt{26}}{2} \sin \theta, \frac{\sqrt{26}}{3} \cos \theta, 0 \bigg) d\theta \\ &= \int_{0}^{2\pi} \bigg(-\frac{26}{6}\sin^2 \theta + \frac{26^{3/2}}{12} \cos^3 \theta \bigg) d\theta \\ &= -\frac{13}{3}\pi \end{align*}
4. Use the Divergence Theorem to find the outward flux of $\vec F$ across the boundary of the region $D$, where $\vec F(x, y, z) = y\, \vec i + xy\, \vec j - z\, \vec k$ and $D$ is the region inside the solid cylinder $x^2 + y^2 \leq 4$, between the plane $z = 0$ and the paraboloid $z = x^2 + y^2$.
Solution¶
We have $\nabla \cdot \vec F = (x-1)$. The solid region is easiest expressed in cylindrical coordinates, so $\nabla\cdot F = (r\cos \theta-1)$, so \begin{align*} \iint \vec F \cdot d \vec S &= \iiint_D (\nabla \cdot \vec F) dV \\ &= \int_{0}^{2\pi} \int_{0}^{2} \int_{0}^{r^2} (r\cos \theta -1) r \ dzdrd\theta \\ &= -8\pi \end{align*}
5. Among all rectangular solids defined by the inequalities $0 \leq x \leq a, 0 \leq y \leq b, 0 \leq z \leq 1$, find the one for which the total flux of $\vec F(x, y, z) = (-x^2 - 4xy) \,\vec i - 6 yz\, \vec j + 12z\, \vec k$ outward through the six sides is the greatest. What is the value of the greatest flux?
First we have $\nabla \cdot F = (-2x -4y) + (-6z) +12$, so \begin{align*} \int_S \vec F \cdot d \vec S &= \int_{0}^{1} \int_{0}^{b} \int_{0}^{a} (\nabla \cdot F) \ dxdydz \\ &= \int_{0}^{1} \int_{0}^{b} \int_{0}^{a} (-2x -4y -6z+12) \ dxdydz \\ &= -a^2b -2ab^2 -3ab + 12ab \\ &= -a^2b -2ab^2 + 9ab \end{align*} To maximize, we take $\nabla(-a^2b -2ab^2 + 9ab) = \langle-2ab -2b^2 +9b, a^2 -4ab+9b\rangle = \vec 0$. Solving for $a $ and $b$ gives, for $a \geq 0$, $b \geq 0$, \begin{align*} &\text{If } a=0 \text{ and } b = 9/2, \text{ then, } -a^2b -2ab^2 + 9ab = 0 \\ &\text{If } a=3 \text{ and } b = 3/2, \text{ then } -a^2b -2ab^2 + 9ab = 27/2 \\ &\text{If } a=9 \text{ and } b = 0, \text{ then } -a^2b -2ab^2 + 9ab = 0 \\ &\text{If } a=0 \text{ and } b = 0, \text{ then } -a^2b -2ab^2 + 9ab = 0 \end{align*} So the maximum flux is $27/2$ and occurs for $a = 3, b= 3/2$.
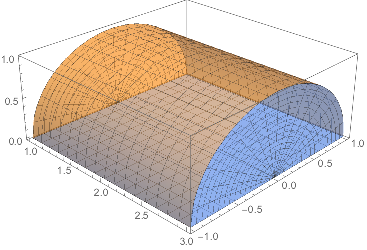
6. Consider the surface $S$ consisteng of the part of the cylinder $y^2+z^2=1$ where $z\geq 0$ and $1\leq x \leq 3$. Find the flux of the vector field $$\vec F(x,y,z) = \tan^{-1}\frac{y}{z+1}\,\vec i + \,x^2\vec j + z\,\vec k $$ upward through $S$ indirectly as follows*.
- Make $S$ into a closed surface by capping its ends with half-discs and its bottom with a rectangle.
- Find the flux through each of these "new" surfaces without actually computing a double integral (i.e., use $\iint_S \vec F\cdot\vec n\,dS$).
- Apply the divergence theorem and draw a conclusion about the flux through the original surface $S$.
*Following this procedure, one should not need to take a single antiderivative.
Solution¶
Let's label the new surfaces $S_1$ for the half-disk cap at $x=1$, $S_2$ the bottom surface, and $S_3$ for the half-disk at $x=3$.
- $S_1$ has outer unit normal vector $-\vec i$. Thus the flux is simply $$\iint_{S_1} -\tan^{-1}\frac{y}{z+1}\,dS$$ which looks awful until we remember that arctan is an odd function and our region in summetric in $y$, so the flux is 0.
- $S_2$ has outer unit normal vector $-\vec k$. Thus the flux is simply $$\iint_{S_2} z \,dS$$ but $z=0$ everywhere on this surface and thus the flux is 0.
- Similarly to the other end, $S_3$ has unit normal $\vec i$. Its flux is $$\iint_{S_3} \tan^{-1}\frac{y}{z+1}\,dS = 0$$ for same reasons as above.
If $E$ is the solid interiar of the half-cuylinder, we compute $$\iiint_E \nabla\cdot \vec F dV = \iiint_E (0 + 0 + 1)\,dV = \text{Vol}(E) = \frac12\pi 2 = \pi$$
We use The Divergence Theorem to put this together, we get $$\iint_S\vec F\cdot d\vec S + \iint_{S_1}\vec F\cdot d\vec S + \iint_{S_2}\vec F\cdot d\vec S + \iint_{S_3}\vec F\cdot d\vec S = \iiint_E \nabla\cdot \vec F dV$$ Since the last three terms on the RHS are all 0, The flux through the top surface is good old $\pi$.