Homework 2¶
Due: January 30, 2018, 8 a.m.¶
Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.
Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.
$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$
1. Suppose $\vec a \ne \vec 0$.
- Suppose $\vec a \cdot \vec b = \vec a \cdot \vec c$. Does it follow that $\vec b = \vec c$?
- Suppose $\vec a \times \vec b = \vec a \times \vec c$. Does it follow that $\vec b = \vec c$?
- Suppose $\vec a \cdot \vec b = \vec a \cdot \vec c$ and $\vec a \times \vec b = \vec a \times \vec c$. Does it follow that $\vec b = \vec c$?
2. Find parametric equations for the following lines:
- the line that goes through the points $(0, -3, 1)$ and $(5, 2, 2)$
the line that goes through the point $(3, 2, 1)$ and is perpendicular to the plane described by the equation $$4x + 3y - 5z = 3.$$
Find equations for the following planes:
- the plane that passes through the point $(1, -1, 1)$ and contains the line with symmetric equations $$x = 2y = 3z.$$
- the plane that contains all points that are equidistant from the points $(3, 2, -1)$ and $(-7, 4, -3)$.
3. Show that if $\langle a, b, c \rangle$ is a unit vector, then the distance between the parallel planes given by $$ ax+by+cz = d_1 ~~~\text{ and }~~~ ax+by+cz = d_2 $$ is $\left|d_1-d_2\right|$. Do not just quote a formula in the text. Use projection.
4. Show that the planes $$ 2x + y -3 z = 4 ~~~\text{ and } ~~~ 4x + 2y -6 z = -2 $$ are parallel and find the distance between the two parallel planes above.
5. (1) Sketch the trace at $z=0$ for each relation below and (2) match the equation with the surface it defines.
| (i) $x = y^2 - z^2$ | (iii) $x^2 = y^2 + z^2$ |
| (ii) $9y^2 + z^2 = 16$ | (iv) $z^2 + x^2 - y^2 = 1$ |
(A) 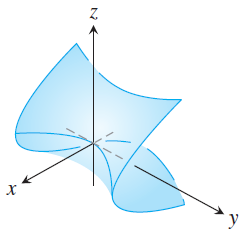 |
(B)  |
(C) 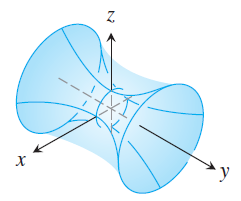 |
(D) 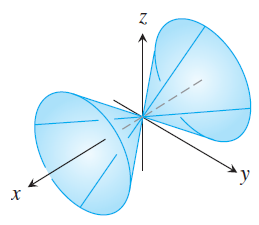 |
6. Find an equation for the surface consisting of all points $P$ for which the distance from $P$ to the $y$-axis is half the distance from $P$ to the $xz$-plane. Sketch or briefly describe the surface.
7. Find paramtric equations for a straight line through the point $(1,1,0)$ that lies entirely on the surface of the hyperboloid $$ x^2+y^2 = z^2 +2. $$