Homework 2

Due: January 30, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1.   Suppose $\vec a \ne \vec 0$.

• Suppose $\vec a \cdot \vec b = \vec a \cdot \vec c$. Does it follow that $\vec b = \vec c$?

  No. For example, let $\vec a = \vec i$, $\vec b = \vec j$, and $\vec c = \vec k$, the standard unit vectors, Each of the latter is orthognal to $\vec a$, but they are certainly not equal.

• Suppose $\vec a \times \vec b = \vec a \times \vec c$. Does it follow that $\vec b = \vec c$?

  No. For example, let $\vec a = \vec i$, $\vec b = \vec j$, and $\vec c = \vec i + \vec j$, then

\begin{align*} \vec a \times \vec b &= \vec i \times \vec j = \vec k \\ \vec a \times \vec c &= \vec i \times (\vec i + \vec j) \\ \ &= \vec i \times \vec i + \vec i \times \vec j = \vec 0 + \vec k = \vec k \end{align*} so these quantities are equal.

• Suppose $\vec a \cdot \vec b = \vec a \cdot \vec c$ and $\vec a \times \vec b = \vec a \times \vec c$. Does it follow that $\vec b = \vec c$?

  Yes. Use linearity. Since $\vec a \times \vec b = \vec a \times \vec c$, then $$ \vec a \times \vec b - \vec a \times \vec c = \vec a \times (\vec b - \vec c) = \vec 0 $$ so we know that $\vec a$ and $\vec b - \vec c$ are parallel. Since $\vec a \ne \vec 0$, we write $$ \vec b - \vec c = k \vec a $$ for some scalar $k$. Now since $\vec a \cdot \vec b = \vec a \cdot \vec c$, we pull the same trick and conclude $$

      \vec a \cdot(\vec b - \vec c) = 0. 
  

  $$ Combining these yields $$

      \vec a \cdot (k \vec a) = k |\vec a|^2 = 0.
  

  $$ Since, $\vec a$ is nonzero, we know $k=0$, so $\vec b - \vec c = \vec 0$.

2. Find parametric equations for the following lines:

• the line that goes through the points $(0, -3, 1)$ and $(5, 2, 2)$

First, we find the vector that goes from the first to the second point: $$ \vec v = \langle 5 -0, 2 - (-3), 2 - 1 \rangle = \langle 5, 5, 1 \rangle. $$ Hence, the line that goes in this direction, and through the point $(0, -3, 1)$ (and the point $(5, 2, 2)$) is $$ \vec r = \langle 0, -3, 1\rangle + t \langle 5, 5, 1 \rangle. $$ Equivalently, a set of parametric equations for the line: $$ x = 5t, ~ y = -3 + 5t, ~ z = 1 + t. $$

• the line that goes through the point $(3, 2, 1)$ and is perpendicular to the plane described by the equation $$4x + 3y - 5z = 3.$$

The normal vector of the plane with equation $4x + 3y - 5z = 3$ is $\vec n = \langle 4, 3, -5\rangle$. This normal vector is perpendicular to the plane. So, we need only to find the equation of a line that goes through the point $(3, 2, 1)$ in the direction $\vec n = \langle 4, 3, -5\rangle$. The line is $$ \vec r = \langle 3, 2, 1 \rangle + t \langle 4, 3, -5 \rangle. $$ Equivalently, a set of parametric equations for this line: $$ x = 3 + 4t, ~ y = 2 + 3t, ~ z = 1 - 5t. $$

Find equations for the following planes:

• the plane that passes through the point $(1, -1, 1)$ and contains the line with symmetric equations $$x = 2y = 3z.$$

The line with the symmetric equations $x = 2y = 3z$ can be rewritten as: $$ x = t, ~ y = \frac{1}{2} t, ~ z = \frac{1}{3} t,$$ or $$ \vec r = t \langle 1, 1/2, 1/3\rangle. $$ So, this line points in the direction $\vec v = \langle 1, 1/2, 1/3\rangle$ and goes through the origin.

The vector from the origin to the point $(1, -1, 1)$ is $\vec u = \langle 1, -1, 1\rangle$. We can find a vector that is orthogonal to the desired plane by taking the cross product of $\vec u$ and $\vec v$: $$ \vec n = \vec v \times \vec u = \langle 5/6, -2/3, -3/2 \rangle. $$ Thus, the equation of the plane: $$ \langle 5/6, -2/3, -3/2\rangle \cdot \langle x, y, z \rangle = 0, $$ or $$ \frac{5}{6}x - \frac{2}{3}y - \frac{3}{2} z = 0. $$

• the plane that contains all points that are equidistant from the points $(3, 2, -1)$ and $(-7, 4, -3)$.

One point that is equidistant from $A (3, 2,-1)$ and $B (-7, 4, -3)$ is the midpoint of the line segment $\overline{AB}$, namely the point $(-2, 3, -2)$. Furthermore, the plane containing all such points must be perpendicular to the direction vector $\overrightarrow{AB} = \langle -10, 2, -2 \rangle$. So, the equation of the plane: $$ \langle -10, 2, -2 \rangle \cdot (\langle x, y, z \rangle - \langle -2, 3, -2 \rangle) = 0, $$ or $$ -10x + 2y - 2z = 30. $$

3. Show that if $\langle a, b, c \rangle$ is a unit vector, then the distance between the parallel planes given by $$ ax+by+cz = d_1 ~~~\text{ and }~~~ ax+by+cz = d_2 $$ is $\left|d_1-d_2\right|$. Do not just quote a formula in the text. Use projection.

Let $\vec v_1 =\langle x_1, y_1, z_1 \rangle$ and $ \vec v_2 = \langle x_2, y_2, z_2 \rangle$ be vectors whose components satisfy the two respective plane equations. Then the distance between the planes is given by \begin{align*} |\proj_{\langle a,b,c\rangle} (\vec v_1- \vec v_2)| &= \left|\frac{\langle a,b,c\rangle \cdot(\vec v_1 - \vec v_2)}{\langle a,b,c\rangle \cdot\langle a,b,c\rangle }\langle a,b,c\rangle\right| \\ \ &= \left|\langle a,b,c\rangle \cdot (\vec v_1- \vec v_2)\right|\frac{|\langle a,b,c\rangle|}{|\langle a,b,c\rangle|^2} \\ \ &= \left|\langle a,b,c\rangle \cdot (\vec v_1- \vec v_2)\right| \\ \ &= |a(x_1 - x_2)+ b(y_1 - y_2) + c(z_1 - z_2)| \\ \ &= |ax_1 + by_1 + cz_1 -(ax_2 + by_2+cz_2)| \\ \ &= |d_1 -d_2| \end{align*} where we used the fact that $|\langle a,b,c\rangle|$ in the third line and the plane equations in the last.

4. Show that the planes $$ 2x + y -3 z = 4 ~~~\text{ and } ~~~ 4x + 2y -6 z = -2 $$ are parallel and find the distance between the two parallel planes above.

Two planes are parallel if their normal vectors are parallel (that is, one is a scalar multiple of the other). The normal vector of the first plane is $\vec n_1 = \langle 2, 1, -3\rangle$; the normal vector of the second plane is $\vec n_2 = \langle 4, 2, -6\rangle$. Note that $\vec n_2 = 2 \vec n_1$. So, the two planes are parallel.

We will find a point in the first plane and a point on the second plane. For example, note that $A (2, 0, 0)$ lies on the first plane and $B (0, -1, 0)$ lies on the second. Then, we project the vector $\overrightarrow{AB} = \langle -2, -1, 0\rangle$ onto the normal vector of the first plane (which is a scalar multiple of the normal vector of the second plane), namely $\vec n_1 = \langle 2, 1, -3 \rangle$. The length of this projection is the distance between the two planes: \begin{eqnarray*} | \proj_{\vec n_1} \overrightarrow{AB} | & = & \frac{|\vec n_1 \cdot \overrightarrow{AB}|}{| \vec n_1|} \\ & = & \frac{|-4 -1 + 0|}{\sqrt{4 + 1 + 9}} = \frac{5}{\sqrt{14}}. \end{eqnarray*}

5. (1) Sketch the trace at $z=0$ for each relation below and (2) match the equation with the surface it defines.

(i) $x = y^2 - z^2$	(iii) $x^2 = y^2 + z^2$
(ii) $9y^2 + z^2 = 16$	(iv) $z^2 + x^2 - y^2 = 1$

(A)	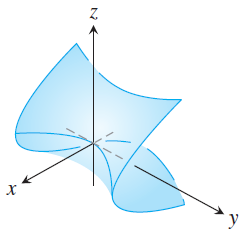(B)
(C)	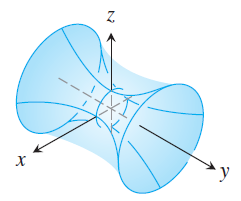(D)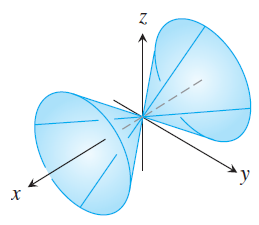

Solutions:

(i)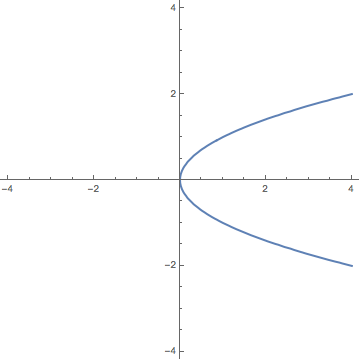

$x = y^2 - z^2$. The trace for $x=k$ is a hyperbola, the trace for $y = k$ is a parabola, and the trace for $z = k$ is also a parabola. In particular, for each fixed $y$, as $z$ goes to $+ \infty$ or $-\infty$, $x$ goes to $-\infty$. For each fixed $z$, as $y$ goes to $+\infty$ or $-\infty$, $x$ goes to $+ \infty$. Thus, this equation corresponds to surface (A), a hyperbolic paraboloid.

(ii)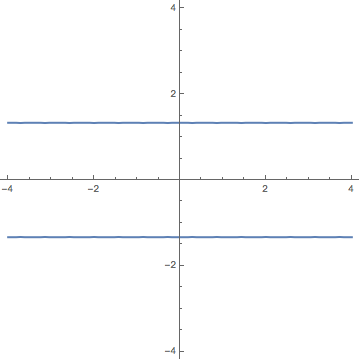

$9y^2 + z^2 = 16$ is a cylinder, whose cross-section parallel to the $yz$-plane is an ellipse. Thus, this equation corresponds to surface (B), an elliptic cylinder.

(iii)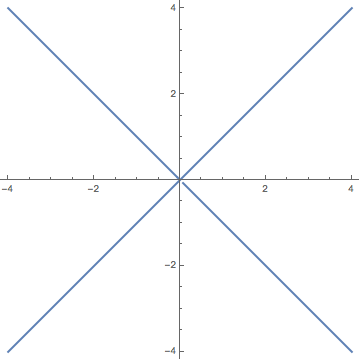

$x^2 = y^2 + z^2$. The trace for $x=k$ is a circle, the trace for $y=k$ is a hyperbola, and the trace for $z=k$ is also a hyperbola. Therefore, the resulting surface is the cone (D).

(iv)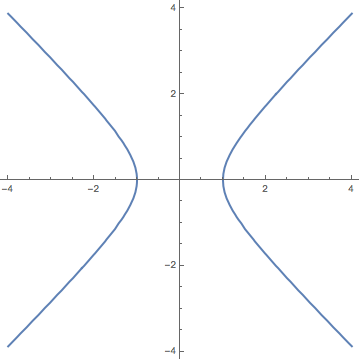

$z^2 + x^2 - y^2 = 1$. The trace for $x = k$ is a hyperbola, the trace for $y = k$ is a circle, and the trace for $z =k$ is a hyperbola. Therefore, the corresponding surface is (C), a hyperboloid of one sheet.

6. Find an equation for the surface consisting of all points $P$ for which the distance from $P$ to the $y$-axis is half the distance from $P$ to the $xz$-plane. Sketch or briefly describe the surface.

The distance of a point $(x, y, z)$ to the $xy$-plane is $|y|$ and its distance to the $y$ axis is $\sqrt{x^2 + z^2}$. Therefore, a point $(x, y, z)$ is on the given surface if and only if $$ \frac{1}{2}|y| = \sqrt{x^2 + z^2}$$ or $$ \frac{y^2}{4} = x^2 + z^2.$$ This equation corresponds to a cone, whose traces in $y=k$ (parallel to the $xz$-plane) are circles of radius $|k|/2$.

7. Find paramtric equations for a straight line through the point $(1,1,0)$ that lies entirely on the surface of the hyperboloid $$ x^2+y^2 = z^2 +2. $$

We have a point on the line, we need only determine a direction vector $\langle a , b , c \rangle$. We recognize to do so, the the line must have form $$ \langle 1,1,0 \rangle + t \langle a,b,c\rangle = \langle 1+ta,1+tb,tc\rangle $$ and thus to satisfy the equation of the surface, we require $$ (1+ta)^2 + (1+tb)^2 = (tc)^2 + 2 $$ for all $t$. Since both sides of this equation are quadratic in $t$, that meantthe corresponding coefficients must be equal. Expanding yields $$ 2+(2a+2b)t+(a^2+b^2)t^2 = 2+c^2 $$ which gives the system \begin{align*} 1+1 &=2 \\ 2a+2b &= 0 \\ a^2 +b^2 &=c^2 \end{align*} As the top equationis trivial, we really have two equations in three unknowns, and we expect to be able to choose one variable freely (this reflects the fact that the direction vector of a line can be any nonzero length).

Set $a=1$. Then, by the second equation, $b=-1$, so $c^2 = 2$. Either root works, so we can choose out line to be $$ \langle1,1,0\rangle + t \langle1,-1,\sqrt{2}\rangle. $$ Any nonzero multiple of this direction vector (or the negative choice for $c$) will work.