Homework 3 Solutions

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1.  

• Find the point on the curve $$\vec r(t) = \langle t^3 + 3t, t^2 + 1, \ln(1 + 2t) \rangle, ~ 0 \leq t \leq \pi,$$ where the tangent line is orthogonal to the plane $$15 x + 4 y + 0.4 z = 10.$$
• Then find the intersection of this tangent line with the plane above.

Solution

• 'Orthogonal to the plane' means the tangent vector to the curve is a multiple of the normal vector to the plane. The derivative is $$\vec r'(t) = \left\langle 3t^2 + 3, 2t, \frac{2}{1 + 2t} \right\rangle,$$ and this direction is tangent to the curve $\vec r(t)$.

The given plane has as a normal vector, the vector $\langle 15, 4, 0.4 \rangle$. Note that $\vec r'(2) = \langle 15, 4, 0.4 \rangle$, which means that the line tangent to the curve at the point $\vec r(2) = \langle 14, 5, \ln(5) \rangle$ is orthogonal to the plane.

The equation of the tangent line: $$ \langle 14, 5, \ln(5)\rangle + t \langle 15, 4, 0.4 \rangle. $$ Plug these components into the equation of the plane and solve for the intersection point in terms of $t$. $$ 15(15t+14)+4(4t+5 + 0.4(0.4t+\ln 5) = 10 $$ so $t = -\frac{10 (550+\log (5))}{6029} \approx -0.915$. So the point of intersection is given by $$ \vec r (-0.915) = \langle 0.275, 1.34, 1.24344 \rangle$$

2. A spaceship, with its engines engaged, has position vector $$ \vec{r}(t) = \left\langle t \cos (t),t \sin (t),a t\right\rangle$$ where $a$ can be set as an arbitrary constant. \] The space station is located at coordinates $\langle -\pi-3,-3\pi,2\rangle$. The captain wants to coast into the space station.

• When should the engines be turned off? (Hint: You can use onely the $x$- and $y$-components to do this)
• What value should $a$ be set to?

Solution

Let $\vec p = \langle -\pi-3,-3\pi,2\rangle $ be the position of the space station. The captain should turn of the engines when the ship's velocity vector is in line with the displacement of the station, or $$ \vec p-\vec r(t) = c\,\vec r'(t) $$ for some $c>0$. We use the first two coordinates to obtain the system \begin{align*} -3-\pi-t\cos t &= c (\cos t -t \sin t) \\ -3\pi - t\sin t &= c (\sin t + t\cos t) \end{align*} This system is quite tricky algebraically, but by trying values per the hint, we see at $t=\pi$: \begin{align*} -3-\pi-(-\pi) &= c (-1) \\ -3\pi &= c (-\pi) \end{align*} is easily solved with $c=3$.

Use the $z$-coordinate to find $a$, using the tangent line at $t=\pi$. $$ 2 -a\pi = 3(a) $$ so $a = \frac{2}{3+\pi}$.

3. Show that a projectile fired from ground attains three-quarters of its maximum height in half the time it takes to reach the maximum height.

Solution

First, we pick our notation. Suppose $\vec r(t)$ denote the projectile's position at time $t$, $v_0$ its initial speed, and $\alpha$ is its launch angle. Suppose that the projectile's initial position is at the origin: $$ \vec r(0) = \langle 0, 0\rangle. $$ Then, its acceleration (due to gravity), velocity, and position vectors are: $$ \vec r''(t) = \langle 0, -g \rangle, ~~~~~ \vec r'(t) = \langle v_0 \cos(\alpha), v_0 \sin(\alpha) - gt \rangle, $$ $$ \vec r(t) = \langle v_0\cos(\alpha) \ t, v_0 \sin(\alpha) \ t - 0.5 gt^2 \rangle.$$

Next, let's figure out its maximum height. The height of the projectile at time $t$ is the $y$-component of $\vec r(t)$: $$ y(t) = v_0 \sin(\alpha) \ t - 0.5 gt^2. $$ Find $t_{\max}$, the time when this maximum height is reached, by setting the first derivative to 0 (i.e., set the $y$-component of the velocity vector to 0): $$ v_0\sin(\alpha) - gt = 0. $$ So, the time it takes to achieve the maximum height is $$ t_{\max} = \frac{v_0 \sin(\alpha)}{g}$$ and the maximum height itself is $$ y_{\max} = v_0 \sin(\alpha) \ \frac{v_0 \sin(\alpha)}{g} - 0.5 g \frac{v_0^2 \sin^2(\alpha)}{g^2} = 0.5 v_0 \sin^2(\alpha)/g.$$

Finally, let's check what height is reached in half the time}:\ The height reached when $t = 0.5 t_{\max} = \frac{v_0 \sin(\alpha)}{2g}$ is \begin{eqnarray*} y(0.5 t_{\max}) & = & v_0 \sin(\alpha) \ \frac{v_0 \sin(\alpha)}{2g} - 0.5 g \frac{v_0^2 \sin^2(\alpha)}{4g^2} \\ & = & \left(\frac{1}{2} - \frac{1}{8}\right)v_0 \sin^2(\alpha)/g\\ & = & \frac{3}{8}v_0 \sin^2(\alpha)/g\\ & = & \frac{3}{4} \times 0.5 v_0 \sin^2(\alpha)/g\\ & = & \frac{3}{4} y_{\max}. \end{eqnarray*} We have shown that a projectile attains three-quarters of its maximum height in half the time it takes to reach its maximum height.

4. Suppose an ant crawls onto the edge of a 12" (diameter) record on a turntable spinning at $33\frac13$ revolutions per minute. A stationary observer looking from above will see its path as motion in the $xy$-plane.

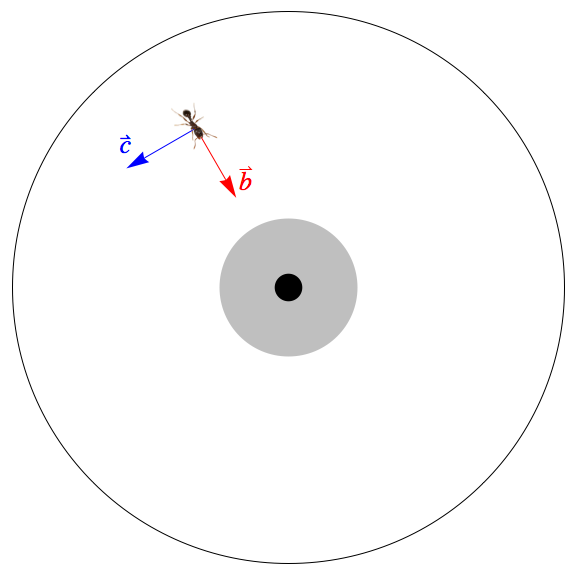
• Suppose the ant stops on the edge of the spinning platter (radius 6"). Find its position, velocity and acceleration relative to the observer as vector-valued finctions of time $t$ in seconds. (You can model its starting position as $\langle 6,0\rangle$ at time $t=0$.)
• Now imagine the ant walks down a radial line of the record toward the center of the turntable. From its perspective, it walks at constant speed and in a straight line, arriving at the center at time $t=45$. Write the ant's position as a vector-valued function of time $t$.
• At any given time $t$, let $\vec b$ be the unit vector pointing from the ant's position toward the center of the turntable, and let $\vec c$ be the unit vector in the direction of the spinning turntable (i.e., perpendicular to $\vec b$). Write the acceleration of the ant as a linear combination of $\vec b$ and $\vec c$.

Solution

• Align the axes so the origin is at the center of rotation and the starting position is $\langle 6,0\rangle$. (This is not the only choice, but it is a sensible one.)

This is simple circular motion. The only notable caveat is that one must traverse the whole circle $33\frac13$ from $t=0$ to $t=60$. Thus, the frequency must be $2\pi\frac{100/3}{60} = \frac{10\pi}{9}$.

\begin{align*} \vec r(t) &= 6\left\langle \cos \frac{10\pi}{9} t,\sin\frac{10\pi}{9} t\right\rangle \\ \vec r'(t) &= \frac{20\pi}{3} \left\langle -\sin \frac{10\pi}{9} t,\cos\frac{10\pi}{9} t\right\rangle \\ \vec r''(t) &= -\frac{200}{27}\pi^2 \left\langle \cos \frac{10\pi}{9} t,\sin\frac{10\pi}{9} t\right\rangle \end{align*} Note, of course, that the acceleration vector points the opposite direction of position, directly toward the center of rotation.

• The key here is that the ant stays on the same radius as in part (a), so its position is simply a scalar multiple of that position. Since we require that the ant move from $6$ to $0$ in 45 seconds, this scalar is simply $6(1-t/45)=6-\frac{2}{15}t$. We get: \begin{align*} \vec r(t) &= (6-\frac{2}{15}t)\left\langle \cos \frac{10\pi}{9} t,\sin\frac{10\pi}{9} t\right\rangle \\ \vec r'(t) &= \left\langle\frac{4}{27} \pi (t-45) \sin \left(\frac{10 \pi t}{9}\right)-\frac{2}{15} \cos \left(\frac{10 \pi t}{9}\right),-\frac{2}{15} \sin \left(\frac{10 \pi t}{9}\right)-\frac{4}{27} \pi (t-45) \cos \left(\frac{10 \pi t}{9}\right)\right\rangle\\ \vec r''(t) &= \frac{8}{243} \pi\left\langle\ 9 \sin \left(\frac{10 \pi t}{9}\right)+5 \pi (t-45) \cos \left(\frac{10 \pi t}{9}\right),5 \pi (t-45) \sin \left(\frac{10 \pi t}{9}\right)-9 \cos \left(\frac{10 \pi t}{9}\right)\right\rangle \end{align*} where we have to be careful with the product rule.

• Here is where a little careful observation can save us a lot of computation. We're reminded from part (a), that the inward pointing vector $\vec b$ has direction $-\langle \cos(2\pi t),\sin(2\pi t)\rangle$. The last equation from part (b) can be written

\begin{align*} \vec a (t) &= \frac{40}{243} \pi ^2 (t-45)\left\langle \cos \frac{10\pi}{9} t,\sin\frac{10\pi}{9} t\right\rangle -\frac{8 \pi }{27} \left\langle -\sin \frac{10\pi}{9} t,\cos\frac{10\pi}{9} t\right\rangle \\ \ &= \frac{40}{243} \pi ^2 (t-45)\vec b -\frac{8 \pi }{27} \vec c \end{align*}