Homework 4

Due: February 13, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. For each function below, (i) identify the domain and range of $f$, and (ii) sketch a contour plot. Draw 5 contours or so at regular intervals of $k$, enough to get the general shape of the graph.

  • $$ f(x,y) = \ln((x-y)^2) $$
  • $$ f(x,y) = \sin(-3x-4y) $$
  • $$ f(x,y) = \frac{2y-x}{x+y+1} $$

2.   Recall that a "hill" can be represented by the graph of the function $$ f(x,y) = e^{-(x^2+y^2)}$$ 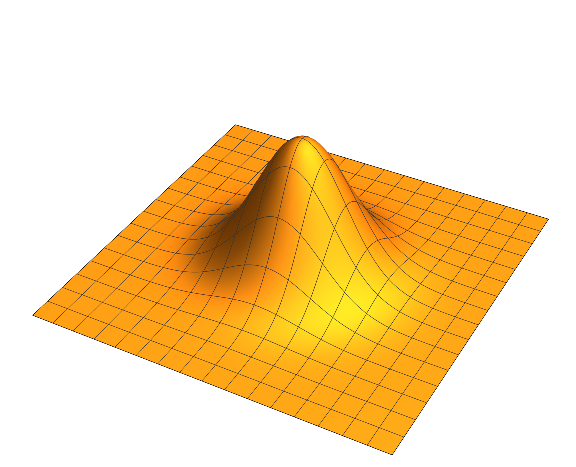A hill

For each of the following "landscapes" find a function who graph resembles the picture in questions.

Try to capture the features but do not worry about an exact match. Use transformations of the function above and experiment with different forms. All pictures were rendered in Mathematica with the following code, where #### is the formula for the function in terms of $x$ and $y$.

Plot3D[ #### ,{x,-5,5},{y,-5,5},PlotRange->Full]
  • "Three peaks of varying widths and heights" 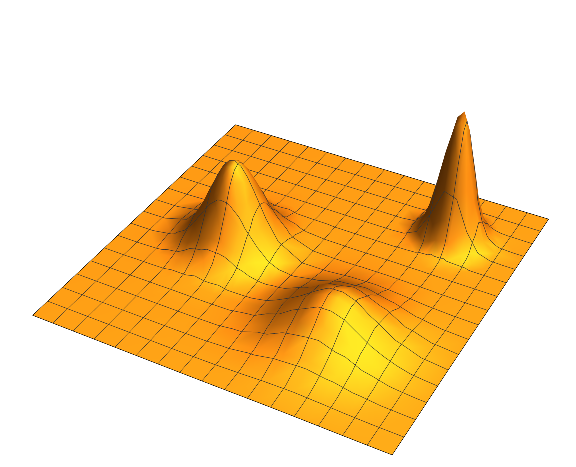3 peaks Hint: Use a sum of transformations of the "hill" above.
  • "A mountain range extendinging infinitely in one direction." 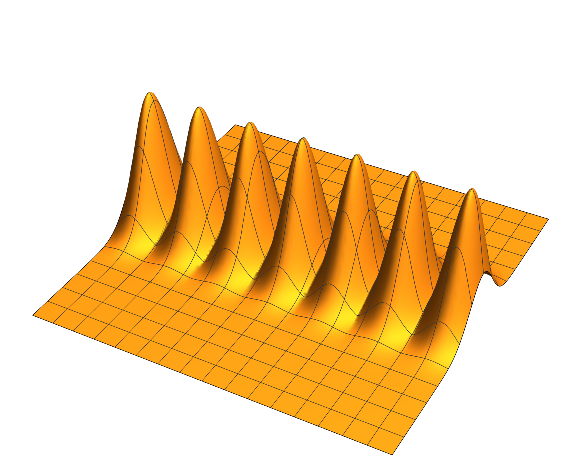A range Do not use and infinite sum here. Use a periodic function.
  • "A canyon." A canyon
  • "A volcano with crater." Use your imagination

3.

  • Use the squeeze theorem to evaluate $$ \lim_{(x,y) \to (0, 0)} \tan(x) \ \sin\left(\frac{1}{|x| + |y|}\right).$$

  • Consider the function $$f(x,y) = \begin{cases} \frac{x^ay^b}{x^2 + y^{2}} & \text{ if } (x,y)\ne (0,0) \\ 0, & \text{ if } (x,y)=(0,0) \end{cases} $$

    where $a, b$ are nonnegative integers.

    For what values of $a$ and $b$ is the function $f$ continuous at $(0, 0)$? (Try some concrete examples like $a=1,b=5$ or $a=0,b=1$ first.)

4. The hyperbolic secant function is defined as $$ \text{sech}(x) = \frac{2}{e^x+e^{-x}}$$

Show that $$u(x,t) = \sqrt{6}\text{sech}(x-t) $$ is a solution to the modified KdV equation $$ u_t +u^2u_x+u_{xxx} =0. $$