Homework 4 Solutions

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. For each function below, (i) identify the domain and range of $f$, and (ii) sketch a contour plot. Draw 5 contours or so at regular intervals of $k$, enough to get the general shape of the graph.

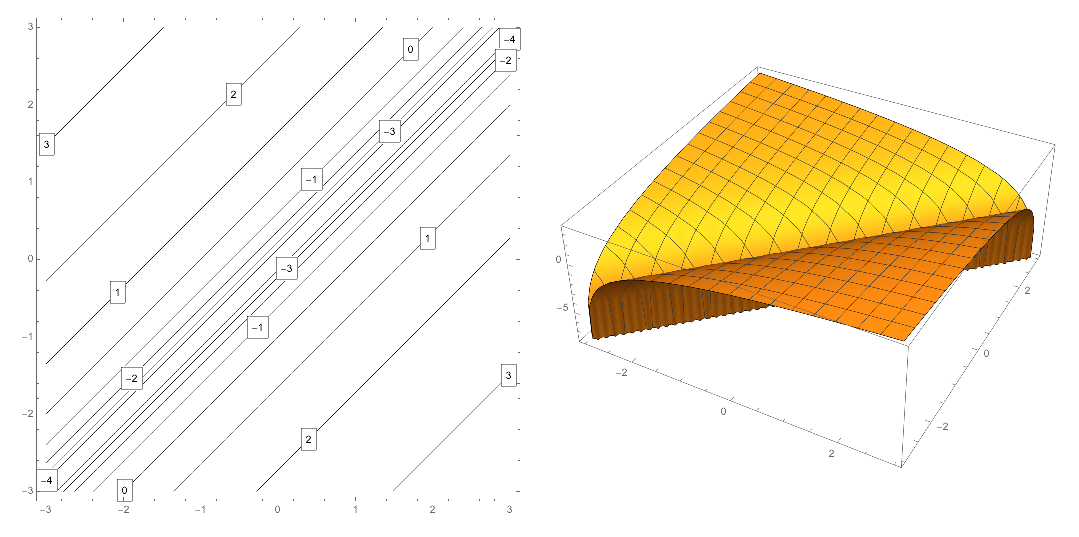
• $$ f(x,y) = \ln((x-y)^2) $$

$\ln$ takes only positive arguments, so the domain is all points such that $(x-y)^2 > 0$, or simply $x\ne y$. Its range is all real values.

Ther level sets are straight lines of the form $y=x\pm e^{k/2}$, so they are tightly crowded about $y=x$ (i.e., where $k<0$).

• $$ f(x,y) = \sin(-3x-4y) $$

The domain is all real numbers. The range is the output of $\sin$, which is the closed interval $[-1,1]$.

A clever way to think about the level curves $f(x,y)=k$ is to recognize the argument of $\sin$ as the dot product $\langle -3,-3,\rangle\cdot\langle x,y\rangle$. Then the level set is all position vector whose dot product with $\langle -3,-4\rangle $ is a constant, more sepcifically, $$ \{(x,y): \langle -3,-4,\rangle\cdot\langle x,y\rangle = \sin^{-1} k + 2\pi n \text{ or } \pi - \sin^{-1} k + 2\pi n \}$$ where $n$ is any integer. This is just a series of lines perpendicular to $\langle -3,-4\rangle$.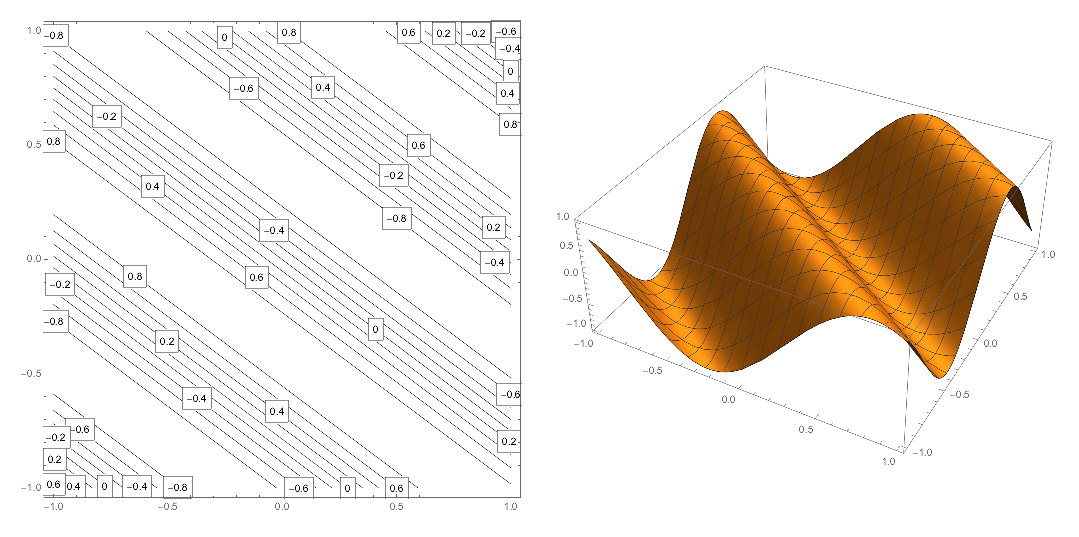

• $$ f(x,y) = \frac{2y-x}{x+y+1} $$

Domain: $D = \{ (x, y) \in \R^2 ~|~ x+ y \neq -1 \}$, since the function is not defined when the denominator is zero. Geometrically, the domain of this function is the set of all points on $\R^2$ except those along the line $y = -1 - x$.

Range = $(-\infty, +\infty)$.

The level curve at height $k$ is a line: $y = -\frac{k+1}{k-2}x -\frac{k}{k-2}$.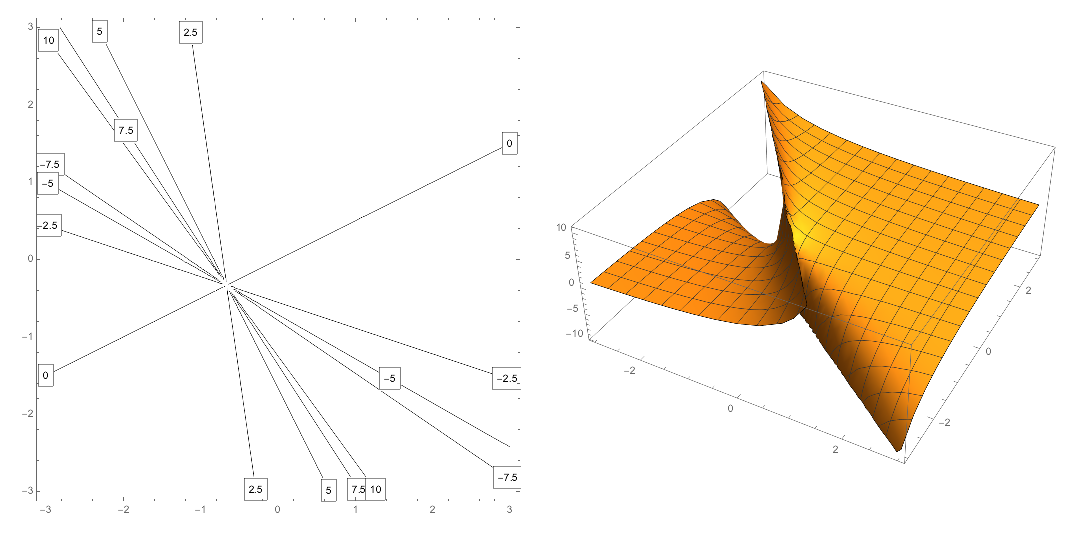

2.   Recall that a "hill" can be represented by the graph of the function $$ f(x,y) = e^{-(x^2+y^2)}$$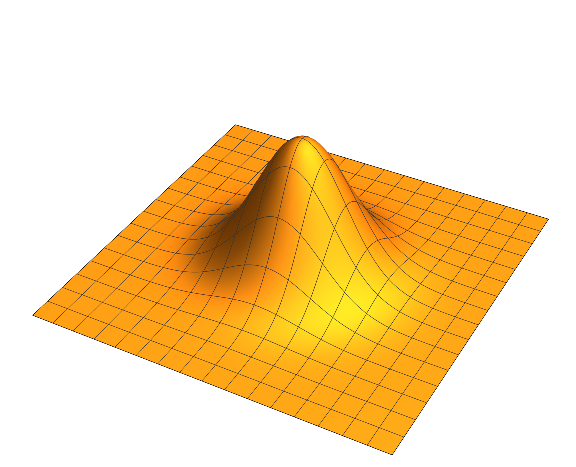

For each of the following "landscapes" find a function who graph resembles the picture in questions.

Try to capture the features but do not worry about an exact match. Use transformations of the function above and experiment with different forms. All pictures were rendered in Mathematica with the following code, where #### is the formula for the function in terms of $x$ and $y$.

Plot3D[ #### ,{x,-5,5},{y,-5,5},PlotRange->Full]

• "Three peaks of varying widths and heights"

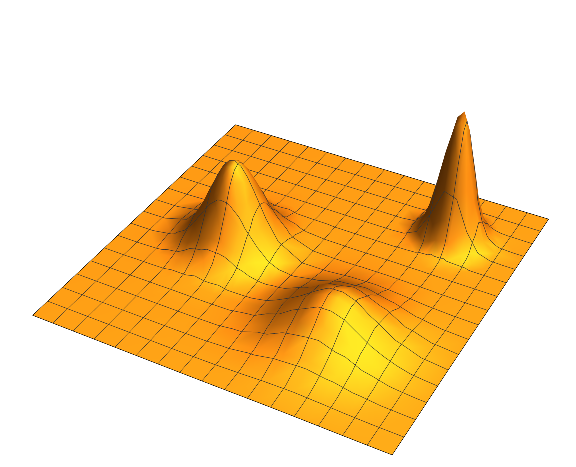
Here we can add three 'hills' where we

translate: $f(x-a,y-b)$

stretch vertically: $Af(x,y)$

stretch horizontally: $f(\omega x, \omega y)$

For example

$$ f(x,y) = 2 e^{-2 \left((x+2)^2+y^2\right)}+4 e^{-3 \left((x-3)^2+(y-3)^2\right)}+e^{\frac{1}{2} \left(-(x-2)^2-(y+2)^2\right)} $$

• "A mountain range extendinging infinitely in one direction."

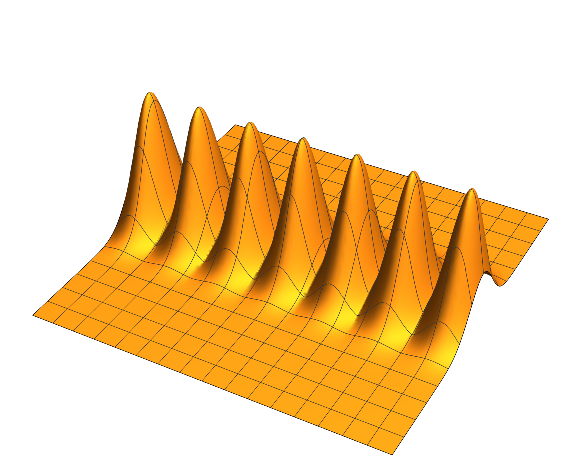
We want to use the hill, but just have the $x$ term hit 0 repeatedly along the $x$-axis. Sine does the trick.

$$f(x,y) = 3 e^{-2 \left(\sin ^2(2 x)+y^2\right)}$$

• "A canyon."

Here, we look for a quantity that is 0 a parabola (like $y=x^2$), grows quickly as one moves away from it, but then levels off. We can thus subtract an exponential from 1 where the argument depends on a quantity like $x-y^2$ $$ f(x,y) = 1 - e^-2(x-y^2)^2. $$

• "A volcano with crater."

  We use a similar idea to part (a), but instead of measuring distance from a line, we can measure deviation from a circle with $x^2+y^2 -1$. Then we form the function \[

          f(x,y) = e^-(x^2+y^2-1)^2
      \\] since this peaks at 1 along the "rim" over the unit circle.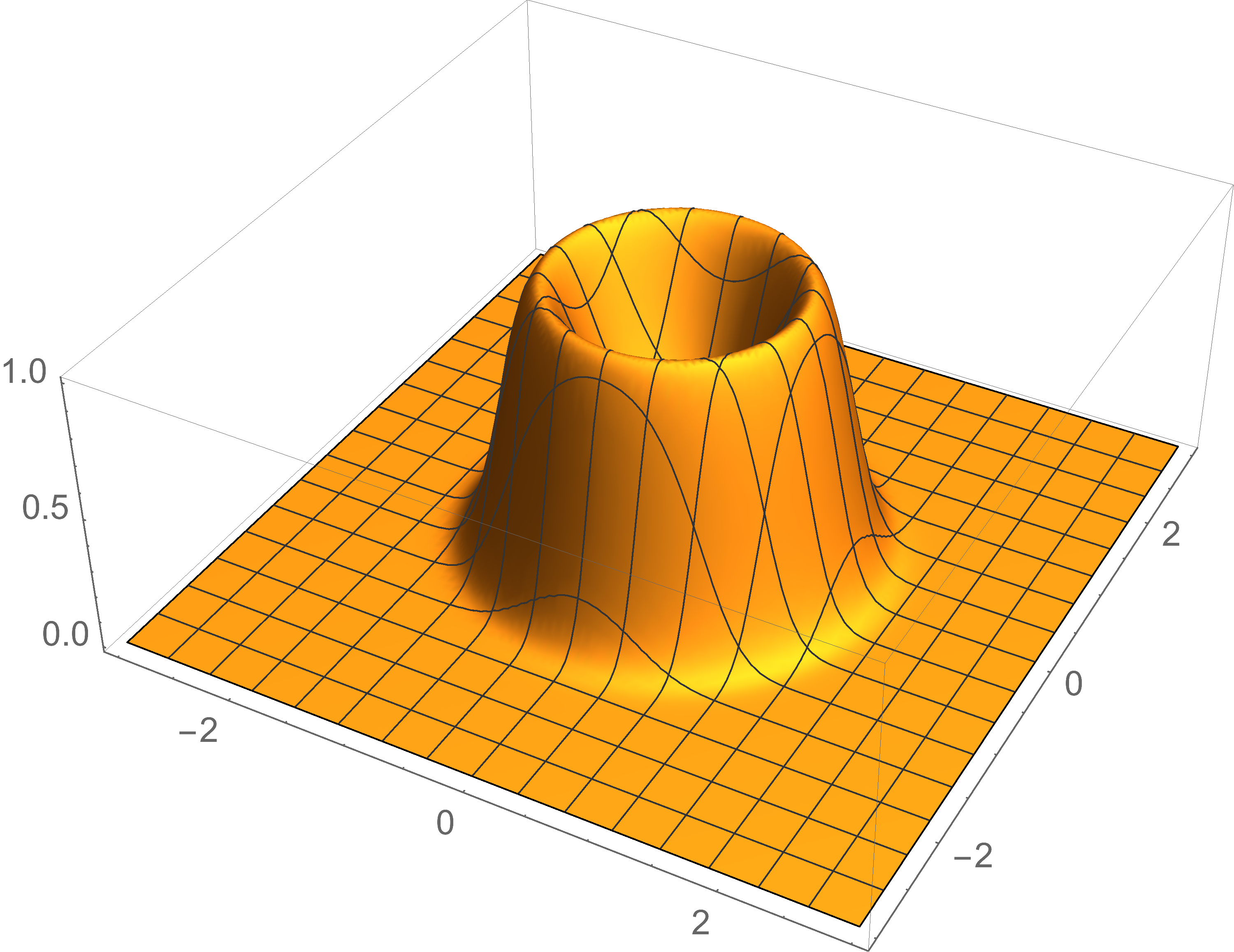 
  

  

3.

• Use the squeeze theorem to evaluate $$ \lim_{(x,y) \to (0, 0)} \tan(x) \ \sin\left(\frac{1}{|x| + |y|}\right).$$

Since the range of sine is $[-1, 1]$, then $0 \leq \left|\sin\left(\frac{1}{|x| + |y|}\right)\right| \leq 1$. So, multiplying by $|\tan(x)|$: $$ 0 \leq \left|\tan(x) \ \sin\left(\frac{1}{|x| + |y|}\right)\right| \leq |\tan(x)|. $$

Taking the limit of both sides of each inequality: $$ \lim_{(x,y) \rightarrow (0, 0)}\ 0 \leq \lim_{(x,y) \rightarrow (0, 0)} \left|\tan(x) \ \sin\left(\frac{1}{|x| + |y|}\right) \right|\leq \lim_{(x,y) \rightarrow (0, 0)} |\tan(x)|. $$

Since $\displaystyle\lim_{(x,y) \rightarrow (0, 0)} |\tan(x)| = 0$, then $$ 0 \leq \lim_{(x,y) \rightarrow (0, 0)} \left|\tan(x) \ \sin\left(\frac{1}{|x| + |y|}\right)\right| \leq 0. $$ By the squeeze theorem, $\displaystyle \lim_{(x,y) \rightarrow (0, 0)} |f(x, y)| = 0$. Since the absolute value is a continuous function, this means that $\displaystyle\lim_{(x, y) \rightarrow (0, 0)} f(x, y) = 0$ as well.

• Consider the function $$f(x,y) = \begin{cases} \frac{x^ay^b}{x^2 + y^{2}} & \text{ if } (x,y)\ne (0,0) \\ 0, & \text{ if } (x,y)=(0,0) \end{cases} $$

  where $a, b$ are nonnegative integers.

  For what values of $a$ and $b$ is the function $f$ continuous at $(0, 0)$? (Try some concrete examples like $a=1,b=5$ or $a=0,b=1$ first.)

The limit of the function $f$ as $(x, y)$ approaches $(0, 0)$ is 0 if $a+b \geq 3$.

Substitute \begin{align*} x &= r \cos \theta \\ y & =r \sin \theta \end{align*}

and compute $$ \lim_{r\to0^+} \left|\frac{(r^a \cos^a\theta)(r^b\sin^b\theta)}{r^2}\right|\le \lim_{r\to0^+} |r|^{a+b-2}. $$ As long as the exponent on the right is positive (i.e., $a+b \ge 3$), this limit converges to 0 by the squeeze theorem.

You can also show that if $a+b$ is not at least 3, then there are paths towards $(0, 0)$ along which $f(x, y)$ approaches different values, hence the limit does not exist.

4. The hyperbolic secant function is defined as $$ \text{sech}(x) = \frac{2}{e^x+e^{-x}}$$

Show that $$u(x,t) = \sqrt{6}\text{sech}(x-t) $$ is a solution to the modified KdV equation $$ u_t +u^2u_x+u_{xxx} =0. $$

First, since we know we'll need 3 derivatives of sech, let's compute them in 1 dimenion (I'll use $y$ as a variable to not confuse it with $x$ and $t$, but clearly it doesn't matter.)

Secondly, to keep our page from getting to be too big a mess, we'll make the following observation. Define

$$ f(y) = e^y + e^{-y} \quad g(y) = e^y - e^{-y} $$

Then, we have the nice relation that $f'(y) = g(y)$ and $g'(y) = f(y)$. Thus as our derivatives repeatedly involve quotient and chain rule, we just keep track of coefficients and powers.

\begin{align*} \text{sech}(y) &= \frac{2}{f(y)} \\ \text{sech}'(y) &= - \frac{2g(y)}{f(y)^2} \\ \text{sech}''(t) &= -2\frac{f(y)^3 - g(y)2f(y)g(y)}{f(y)^4} \\ \ &= -2\frac{1}{f(y)} + 4\frac{g(y)^2}{f(y)^3} \\ \text{sech}'''(t) &= \frac{2g(y)}{f(y)^2} + 4\frac{2g(y)f(y)f(y)^3 - g(y)^2 3f(y)^2g(y)}{f(y)^6} \\ \ &= 2\frac{g(y)}{f(y)^2} + 8\frac{g(y)}{f(y)^2} - 12\frac{g(y)^3}{f(y)^4} \\ \ &= 10\frac{g(y)}{f(y)^2} - 12\frac{g(y)^3}{f(y)^4} \end{align*}

Now we recognize the crucial fact that when computing partial derivatives of $\text{sech}(x-t)$, we have from the chain rule \begin{align*} \partial_t \text{sech}(x-t) &= - \text{sech}'(x-t) \\ \partial_x \text{sech}(x-t) &= \text{sech}'(x-t) \\ \end{align*}

So now we can expand the terms of our PDE in terms of $f$ and $g$ and just recognize that differentiating with respect to $t$ bring a minus sign, but with respect to $x$ does not. \begin{align*} u_t &= 2\sqrt{6}\frac{g}{f^2} \\ u^2u_x &= \left( \sqrt{6} \frac{2}{f} \right)^2\left( -\sqrt{6} \frac{2g}{f^2} \right) \\ \ &= -48\sqrt{6}\frac{g}{f^4} \\ u_{xxx} &= 10\sqrt{6}\frac{g}{f^2} -12\sqrt{6}\frac{g^3}{f^4} \end{align*}

Eliminate the $\sqrt{6}$ term and put over a common denominator of $f^4$ leaves a numerator of $$ 12g f^2 -48g -12g^3 = 12g(f^2-4-g^2) = 12g((f+g)(f-g)-4) = 12g((2e^y)(2e^{-y})-4)=0 $$