Homework 5 Solution

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. A friend was asked to find the equation of the tangent plane to the surface $z = x^3 - \arctan (y-1) $ at the point $(x, y) = (2, 1)$. The friend's answer was $$z = 3x^2(x-2) - \frac{1}{2-2y+y^2}(y-1)+8.$$

• At a glance, without doing any computation, how do you know that this is incorrect? What mistake did the friend make?
• Answer the question correctly.

Solution

• This equation is not a linear equation! The friend left the general form of the partial deriivatives, failing to evaluate them at the point in question.
• The equation is $z = 12(x-2) - (y-1) +8 = 12x-y-15$ (i.e. evaluate the partial derivatives at $(x, y) = (2, 1)$).

2. Estimate the quantity $$ \frac{8.01}{\sqrt{1.99\times2.01}} $$ "by hand" using a technique similar to that done in class.

Solution

We linearize the function $f(x,y,z) = \frac{x}{\sqrt{yz}}$ around the point $(8,2,2)$.

$$f(x,y,z)\approx f(8,2,2)+f_x(8,2,2)\Delta x +f_y(8,2,2)\Delta y +f_z(8,2,2)\Delta z$$ $$ = 4+\frac12(0.01)+(-1)(-0.01) + (-1)(0.01) = 4.005 $$ where the Mathematica answer is given by $4.00505$.

3.  Let $$ f(x,y) = \ln (y-x^2) $$

• Find $L(x,y)$, the linearization of $f$ around the point $(0,1)$ and show that $L$ has the same first-order partial derivatives as $f$ at that point.
• Find constants $a_1,\ldots,a_6$ such that the function $$M(x,y) = a_1 + a_2x +a_3y +a_4x^2 +a_5 xy +a_6 y^2$$ has the same
  • value,
  • first-order partial derivatives, and
  • second-order partial derivatives as $f$ at $(0,1)$.

Solution

\begin{align*} L(x,y) &= f(0,1)+f_x(0,1)(x)+f_y(0,1)(y-1) \\ &= 0 - \left.\frac{2x}{y-x^2}\right|_{0,1} (x) + \left.\frac{1}{y-x^2}\right|_{0,1} (y-1) \\ &= y-1 \end{align*}

For the second part, we start with the second-order derivatives. \begin{align*} f_{xx}(x,y) &= -\frac{2(y-x^2) + 2x(2x)}{(y-x^2)^2} = -2\frac{y+x^2}{(y-x^2)^2} \\ f_{xy}(x,y) &= \frac{2x}{(y-x^2)^2} \\ f_{yy}(x,y) &= -\frac{1}{(y-x^2)^2} \\ \end{align*}

evaluating at $(0,1)$ gives values of $-2,0,1$, repectively. We then match these up with $M$. \begin{align*} -2 &=M_{xx}(0,1) = 2a_4 \\ 0 &= M_{xy}(0,1) = a_5 \\ -1 &= M_{yy}(0,1) = 2a_6 \end{align*}

Plug into $M$ and check first derivatives against results for $f$ above. \begin{align*} 0 &= f_x(0,1) = M_{x}(0,1) = a_2 + a_5 = a_2 \\ 1 &= f_y(0,1) =M_{y}(0,1) = a_3 + 2 a_6 \\ \end{align*} and lasty check the value itself. $$0=f(0,1) = M(0,1) = a_1+a_3+a_6 $$

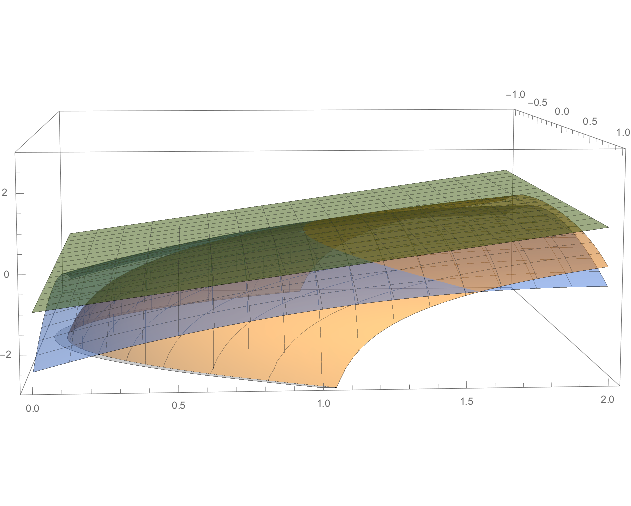
So, $$M(x,y)= -\frac32 + 2y -x^2 -\frac12y^2 $$

Here is the graph of the function, its tangent plane and the "best fit quadratic":

4. Find the value of $\partial x/\partial z$ at the point $(1, -1, -3)$ if the equation $$ xz + y \ln(x) - x^2 + 4 = 0$$ defines $x$ as a function of the two independent variables $y$ and $z$.

Solution

Let $F(x,y,z) = xz + y \ln(x) - x^2 + 4$ $$ \frac{\partial x}{\partial z} = -\frac{F_z}{F_x} = \frac{x}{z + y/x - 2x} $$ Evaluating at $(1,-1,-3)$ yields $\frac16$.

5. If $f(u, v, w)$ is differentiable and $u = x-y, v= y-z$, and $w = z-x$, show that $$ \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} + \frac{\partial f}{\partial z} = 0. $$

Solution

\begin{align*} \frac{\partial f}{\partial x} & = \frac{\partial f}{\partial u} \ \frac{\partial u}{\partial x} + \frac{\partial f}{\partial v} \ \frac{\partial v}{\partial x} + \frac{\partial f}{\partial w} \ \frac{\partial w}{\partial x} \\ & = \frac{\partial f}{\partial u} + 0 - \frac{\partial f}{\partial w} \\ \ \\ \frac{\partial f}{\partial y} & = \frac{\partial f}{\partial u} \ \frac{\partial u}{\partial y} + \frac{\partial f}{\partial v} \ \frac{\partial v}{\partial y} + \frac{\partial f}{\partial w} \ \frac{\partial w}{\partial y} \\ & = -\frac{\partial f}{\partial u} + \frac{\partial f}{\partial v} + 0 \\ \ \\ \frac{\partial f}{\partial z} & = \frac{\partial f}{\partial u} \ \frac{\partial u}{\partial z} + \frac{\partial f}{\partial v} \ \frac{\partial v}{\partial z} + \frac{\partial f}{\partial w} \ \frac{\partial w}{\partial z} \\ & = 0 - \frac{\partial f}{\partial v} + \frac{\partial f}{\partial w} \\~\\ \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} + \frac{\partial f}{\partial z} & = \left(\frac{\partial f}{\partial u} - \frac{\partial f}{\partial w}\right) + \left(-\frac{\partial f}{\partial u} + \frac{\partial f}{\partial v}\right) + \left(-\frac{\partial f}{\partial v} + \frac{\partial f}{\partial w}\right) = 0. \end{align*}

6. A function $f(x, y)$ is called homogeneous of degree $p$ if $$ f(tx, ty) = t^p f(x, y)$$ for all $t$. Show that any differentiable, homogeneous function of degree $p$ satisfies Euler's Theorem: $$ x f_x(x, y) + y f_y(x, y) = p f(x, y). $$ Hint: Define $g(t) = f(tx, ty)$ and compute $g'(1)$.

Solution

The hint is everything. \begin{align*} g'(t) &= \frac{d}{dt} f(tx,ty) = f_x(tx,ty) \frac{d}{dt}(tx) + f_y(tx,ty) \frac{d}{dt}(ty) \\ &= x f_x(tx,ty) + y f_y(tx,ty) \\ &= \frac{d}{dt} t^p f(x,y) = pt^{p-1} f(x,y) \end{align*} Setting $t=1$ on the RHS of lines 2 and 3 gives the result.