Homework 6

Due: February 27, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. Let $f(x, y) = \frac{x+y}{1+x^2}$. Find the directional derivative of $f$ at the point $(1, -2)$ in the direction of:

• $\vec u = 3\,\vec i - 2\,\vec j$
• $\vec v = -\vec i + 4\,\vec j$

Solution

$$\nabla f(x, y) = \langle f_x(x, y), f_y(x, y) \rangle = \langle \frac{1-x^{2}-2xy}{(1+x^{2})^{2}}, \frac{1}{(1+x^{2})} \rangle$$

$$\nabla f(1,-2) = \langle 1,\frac12 \rangle$$

• So, the directional derivative of $f$ at $(1, -2)$ in direction $\vec u = \frac{\vec v}{|\vec v|} = \frac{1}{\sqrt{13}}\langle3,-2\rangle$ is \begin{eqnarray*} D_{\vec u}f(1, -2) & = & \nabla f(1, -2) \cdot \vec u\\ & = & \frac{2}{\sqrt{13}}. \end{eqnarray*}

• The directional derivative of $f$ at $(1, -2)$ in direction $\vec u = \frac{\vec v}{|\vec v|} = \frac{1}{\sqrt{17}}\langle-1,4\rangle$ is \begin{eqnarray*} D_{\vec u}f(1, -2) & = & \nabla f(1, -2) \cdot \vec u \\ & = & \frac{1}{\sqrt{17}} \end{eqnarray*}

2. a. Two surfaces are called \textbf{orthogonal} at a point of intersection if their normal lines are perpendicular at that point.

Show that surfaces with equations $F(x, y, z) = 0$ and $G(x, y, z) = 0$ are orthogonal at a point $P$ where $\nabla F \neq 0$ and $\nabla G \neq 0$ if and only if at the point $P$, $$ F_x G_x + F_y G_y + F_zG_z = 0. $$

Solution

Suppose that $P = (x_0, y_0, z_0)$ is a point in the intersection of $F(x, y, z) = 0$ and $G(x, y, z) = 0$. Then, $\nabla F(x_0, y_0, z_0) = \langle F_x, F_y, F_z\rangle$ is a vector that is normal to the surface $F(x, y, z) = 0$ at $P$. Similarly, $\nabla G(x_0, y_0, z_0) = \langle G_x, G_y, G_z\rangle $ is a vector that is normal to the surface $G(x, y, z) = 0$ at $P$.

If the two surfaces are orthogonal at $P$, then their normal vectors are orthogonal at $P$. In other words, $$ \nabla F(x_0, y_0, z_0) \cdot \nabla G(x_0, y_0, z_0) = 0 $$ or $$ F_x G_x + F_yG_y + F_z G_z = 0.$$

Conversely, if $F_x G_x + F_yG_y + F_z G_z = 0$, then the normal vectors are orthogonal to one another at $P$, which implies that the two surfaces are orthogonal to one another.

b. Use part a. to show that the surfaces $z^2 = x^2 + y^2$ (a cone) and $x^2 + y^2 + z^2 = r^2$ (a sphere) are orthogonal at every point of intersection.

Solution

Let $F(x, y, z) = z^2 - x^2 - y^2$ and $G(x, y, z) = x^2 +y^2 + z^2 - r^2$. Then, $$ \nabla F (x, y, z) = \langle -2x, -2y, 2z \rangle, $$ $$ \nabla G (x, y, z) = \langle 2x, 2y, 2z \rangle. $$

Consider a point $(x_0, y_0, z_0)$ on the intersection. Note that $$ \nabla F(x_0, y_0, z_0) \cdot \nabla G(x_0, y_0, z_0) = -4x_0^2 - 4y_0^2 + 4z_0^2.$$ Since $(x_0, y_0, z_0)$ lies on the intersection, it satisfies $F(x_0, y_0, z_0) = 0$ and $G(x_0, y_0, z_0) = 0$. In particular, since $F(x_0, y_0, z_0) = 0$, then it must be the case that $z_0 = x_0^2 + y_0^2$.

So, $$ \nabla F(x_0, y_0, z_0) \cdot \nabla G(x_0, y_0, z_0) = -4x_0^2 - 4y_0^2 + 4(x_0^2 + y_0^2) = 0.$$ By part (a), the two surfaces are orthogonal at the point $(x_0, y_0, z_0)$. Since this is an arbitrary point on the intersection of the two surfaces then the two surfaces are in fact orthogonal at every point in the intersection.

3.  Consider the function $f(x,y)=x^2 - \frac{y^2}{9}$.

a. Sketch a contour plot with (at least) levels $k=0,\pm1,\pm2,\pm3$. Plot a point at $(2,6)$ and roughly sketch a ``path of greatest descent'' starting from this point. That is, a path along which the directional derivative is as low a number as possible.

Solution

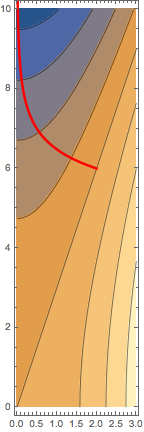
b. Find a formula for your curve in part a. That is, find a curve $\vec r(t) = \langle x(t),y(t)\rangle$ such that $$ -\nabla f = \vec r'(t) $$ and $\vec r(0) = \langle 2,6 \rangle$. (This is technically an ODE, but one you can solve.)

Solution

We're looking for a function of the form $\vec r(t) = \langle x(t),y(t) \rangle $. that satisfies the equation above at each point. Since $\nabla f(x,y) =\langle 2x,\frac29 y\rangle$, we have:

$$ \begin{bmatrix} x'(t) \\ y'(t)\end{bmatrix} = \begin{bmatrix} -2x(t) \\ \frac29 y(t)\end{bmatrix} $$

where $x(0) = 2$ and $y(0) = 6$. These are separable ODEs (see Stewart $\S9.3$, for example).

$$ \begin{bmatrix} x(t) \\ y(t)\end{bmatrix} = \begin{bmatrix} 2e^{-2t}) \\ 6e^{\frac29 t} \end{bmatrix} $$

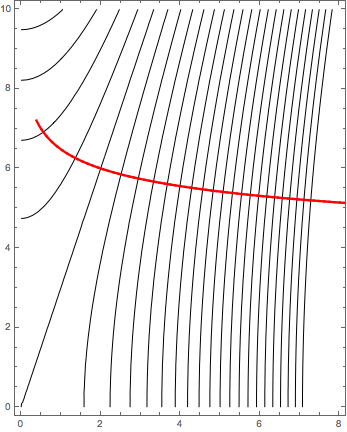
c. In your curve from part b, solve for $y$ in terms of $x$ and plot the function. Is it close to your guess from part a?

Solution

We have $y = 6e^{2/9 t} = 6e^{(-2t)(-1/9)} = 6\sqrt[9]{\frac{2}{x}}$. Does resemble the above:

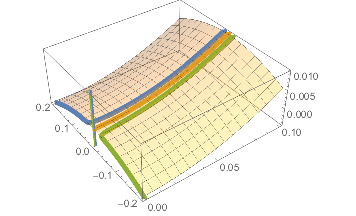
d. Compare, qualitatively, what happnes to the limit $$\lim_{t\to\infty} \vec r(t) $$ in the three cases:

• $ \vec r(0) = \langle 10,.01\rangle$
• $\vec r(0) = \langle 10,0\rangle$
• $\vec r(0) = \langle 10,-.01\rangle$

Solution

The only difference with the above is the initial point $\vec r(0)$. Its components show up as the coefficients in front of the exponentials. Thus, for all three starting points, the $x$-coordinate is $10e^-2t$ which goes to 0 as $t \to\infty$. Now taking the three cases for the $y$-coordinate we see :

• $.01 e^{\frac29 t}$ which heads to $+\infty$ as $t\to\infty$
• $0$ for all $t$
• $-.01 e^{\frac29 t}$ which heads to $-\infty$ as $t\to\infty$

So the middle case is a path that converges toward the origin and the the others run aways from it in opposite directions.

Here are the three paths composed with the function, near the origin: