Homework 7¶
Due: March 6, 2018, 8 a.m.¶
Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.
Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.
$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$
1. Consider the function $$f(x, y) = 2 x^2+y^2 - k xy$$ where $k$ is some fixed constant.
a. Show that for any value of $k$, $(0, 0)$ is a critical point of $f$.
b. Determine the values of $k$ (if any) for which $(0, 0)$ is
- a saddle point,
- corresponds with a local maximum,
- corresponds with a local minimum.
2. Show that the point $(c,d)$ for which the sum of the squares of the distances to a set of fixed points $(a_1,b_1),(a_2,b_2),\ldots,(a_n,b_n)$ is minimized is located such that $c$ is the average of the $a$-coordinates and $d$ is the average of the $b$-coordinates.
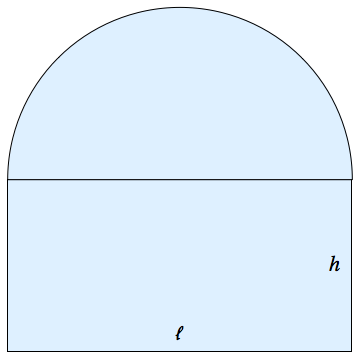
3. A region in the plane consist of a semicircle sitting atop a rectangle. If the perimeter is fixed and the area is maximized, find the ratio $\frac{\ell}{h}$ of the sides of the rectangle.
4. A solid sphere $x^2+y^2+z^2\le1$ has a temperature distribution given by $$ T(x,y,z) = e^{-((2+5x)^2+(1-5y)^2+(2-5z)^2)} $$ Find its hottest and coldest temperatures.
5. Consider the problem of minimizing the function $f(x, y) = x$ on the curve $y^2 + x^4 - x^3 = 0$ (a type of curve known as a "piriform"). 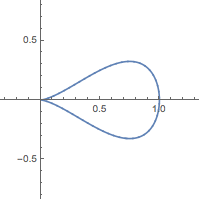
a. Try using Lagrange multipliers to solve the problem.
b. Show that the minimum value is $f(0, 0)$ even though the Lagrange condition $\nabla f(0, 0) = \lambda \nabla g(0, 0)$ is not satisfied for any value $\lambda$.
c. Briefly explain (1–2 sentences) why Lagrange multipliers fail to find the minimum value in this case.