Homework 7 Solution

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. Consider the function $$f(x, y) = 2 x^2+y^2 - k xy$$ where $k$ is some fixed constant.

  a. Show that for any value of $k$, $(0, 0)$ is a critical point of $f$.

Solution

We compute $$ \nabla f(x,y) = \begin{bmatrix} 4x - k y \\ 2y - k x \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$ if $x=y=0$.

  b. Determine the values of $k$ (if any) for which $(0, 0)$ is

• a saddle point,
• corresponds with a local maximum,
• corresponds with a local minimum.

Solution

We run the second derivative test. $$ D = \begin{vmatrix} 4 & -k \\ -k & 2 \end{vmatrix} = 8-k^2 $$

This is quadratic in $k$ of course and is negative if $k>2\sqrt2$ or $k < -2\sqrt2$, thus $(0,0)$ is a saddle point for $k$ in this range. If $-2\sqrt2 <k<2\sqrt 2$, $D>0$ and sice $f_xx >0$, there is a local minimum at the origin in these cases. This leaves the boundary cases $k^2=8$. We need another method, but in these cases, $f$ factors. $$ 2x^2+y^2 \pm 2\sqrt2 x y = (\sqrt 2 x \pm y)^2 \ge 0 $$ so $f(0,0)$ is a local minimum in these cases as well.

2. Show that the point $(c,d)$ for which the sum of the squares of the distances to a set of fixed points $(a_1,b_1),(a_2,b_2),\ldots,(a_n,b_n)$ is minimized is located such that $c$ is the average of the $a$-coordinates and $d$ is the average of the $b$-coordinates.

Solution

The only difficulty here is unpacking the wording. The thing we're minimizing is the "sum of squares of distances to ..." so the variables we control are the coordinates of the point $(c,d)$. So we set up a function $$ f(c,d) = \sum_{i=1}^n \text{distance}((c,d),(a_i,b_i))^2 $$ $$ = \sum_{i=1}^n (c-a_i)^2 + (d-b_i)^2 $$

$(c,d)$ are unconstrained and can be technically anything, so we look for critical points.

$$ \nabla f(c,d) = \begin{bmatrix} \sum_{i=1}^n 2(c-a_i) \\ \sum_{i=1}^n 2(d-b_i) \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$

Looking at the first equation, we have $\sum_{i=1}^n 2(c-a_i) = 0$ we can divide both sides by 2 to get rid of it. The by splitting the two parts of the sum, we have $$ \sum_{i=1}^n c - \sum_{i=1}^n a_i = 0 $$ $$ nc - \sum_{i=1}^n a_i = 0 $$

Finally solving for $c$, we have $$ c = \frac{\sum_{i=1}^n a_i}{n} $$ which is the average of the $a_i$'s. Similary, $$ d = \frac{\sum_{i=1}^n b_i}{n} $$ which is what we were to show.

A formal argument for this having a global minimum is a bit involved (and unnecessary). Suffice to say a sum of distances will diverge to infinity as the point moves out to infinity, and is bounded below by 0, so it must have a minimum. This minimum must occur at a critical point, and so we have found it.

3. A region in the plane consist of a semicircle sitting atop a rectangle. If the perimeter is fixed and the area is maximized, find the ratio $\frac{\ell}{h}$ of the sides of the rectangle.

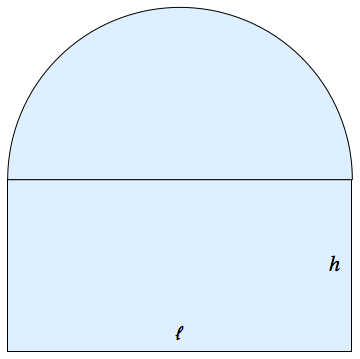
Solution

This is a classic Lagrange problem.

Function to be maximized (area): $$A(\ell,h) = \ell h + \frac\pi8 \ell^2 $$

Constraint (perimeter): $$P(\ell,h) = \ell + 2h + \frac\pi2\ell = k$$ for some fixed quantity $k$.

We look for "Lagrange points" $$\nabla A = \begin{bmatrix} h+\frac\pi4 \ell \\ \ell \end{bmatrix} = \lambda \begin{bmatrix} 1+\frac\pi2 \\ 2 \end{bmatrix} = \lambda \nabla P$$

Dividing both sides of this equation (we can because $\ell = 0$ clearly fails the constraint) gives $$\frac{h+\frac\pi4\ell}{\ell} = \frac{1+\frac\pi2}{2} n$$

$$\frac h\ell +\frac\pi4 = \frac12 +\frac\pi4$$

Canceling the last term on each side gives the result.

4. A solid sphere $x^2+y^2+z^2\le1$ has a temperature distribution given by $$ T(x,y,z) = e^{-((2+5x)^2+(1-5y)^2+(2-5z)^2)} $$ Find its hottest and coldest temperatures.

Solution

We'll certainly need the termperature gradient.

$$ \nabla T(x,y,z) = -10 e^{\left(-(5 x+2)^2-(1-5 y)^2-(2-5 z)^2\right)}\begin{bmatrix} 5 x+2 \\ 5 y-1 \\ 5 z-2 \end{bmatrix} $$

We first look for critical points. Per the hint, the exponential term is never zero, so we need only solve \begin{align*} 5x+2 &=0 \\ 5y-1 &= 0 \\ 5z-2 \end{align*} so $\left(\frac25,\frac15,\frac25\right)$ is the sole critical point. This is clearly inside the sphere, so it is a candidate.

Next, we need to check the boundary of region. That is, where $ x^2+y^2+z^2 =1$. Taking the LHS as a (surface-defining) function $g$, we set up a Lagrange multipliers problem and solve $$ -10 e^{\left(-(5 x+2)^2-(1-5 y)^2-(2-5 z)^2\right)}\begin{bmatrix} 5 x+2 \\ 5 y-1 \\ 5 z-2 \end{bmatrix} = \lambda \begin{bmatrix} 2x \\2y \\2z \end{bmatrix} $$

Now, we can get a little clever with the algebra. We're really looking for where the two vectors point in the same direction so we can effectively ignore the scalar multiple on the left, or "absorb it into $\lambda$." (Put another way, if we solve each equation for \lambda, the big exponential terms cancel out on all sides of the equation.) We thus have

\begin{align*} 5 x+2 &= 2\lambda x \\ 5 y-1 &= 2\lambda y \\ 5 z-2 &= 2\lambda z \end{align*}

Rearranging, we have $$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \frac{1}{5-2\lambda} \begin{bmatrix} -2 \\ 1 \\ 2 \end{bmatrix} $$

So $\langle x,y,z\rangle$ is a miltiple of $\langle -2,1,2\rangle$, but there are only 2 on the unit sphere:

$$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \pm\frac{1}{3} \begin{bmatrix} -2 \\ 1 \\ 2 \end{bmatrix}$$

Finally, we can test our points. \begin{align*} T(-2/5,1/5,2/5) &= 1 \\ T(-2/3,1/3,2/3) &= e^{-4} \\ T(2/3,-1/3,-2/3) &= e^{-64} \\ \end{align*} So, the first point is the hottest and the last the coldest.

For no real reason, here's a gif of the level sets of $T$ with the unit sphere.

5.  Consider the problem of minimizing the function $f(x, y) = x$ on the curve $y^2 + x^4 - x^3 = 0$ (a type of curve known as a "piriform").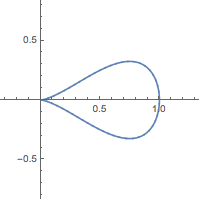

  a. Try using Lagrange multipliers to solve the problem.

Solution

The system of equations is: \begin{align*} 1 & = \lambda (4x^3 - 3x^2) \\ 0 & = 2 \lambda y\\ y^2 + x^4 - x^3 & = 0 \end{align*} The first constraint implies that $\lambda \neq 0$ and $x \neq 0$. So, in the second constraint, it must be the case that $y=0$.

Since $y=0$, then we can use the third constraint to solve for $x$: $x^4 - x^3 = 0$, which means that $x = 0$ or $x = 1$. Since $x$ cannot equal $0$, then the only solution for $x$ is $x = 1$.

So, the only solution is $(1, 0)$, with value $f(1, 0) = 1$. However, $(1, 0)$ cannot be the point that minimizes $f$. For instance, the point $(0, 0)$ satisfies the constraint and $f(0, 0) = 0$, which is smaller.

  b. Show that the minimum value is $f(0, 0)$ even though the Lagrange condition $\nabla f(0, 0) = \lambda \nabla g(0, 0)$ is not satisfied for any value $\lambda$.

Solution

To show that $f(0, 0) = 0$ is the minimum, we must show that if $f(x, y) = x <0$, then there is no $y$ that satisfies $y^2 + x^4 - x^3 = 0$:

If $x<0$, then $x^3<0$ and $x^4 > 0$. So, $y^2 = x^3 - x^4 <0$. So, $y$ has no real-valued solution.

So, $f(x, y) = x = 0$ is the smallest possible value of $f$ in the region specified by the constraint.

  c. Briefly explain (1–2 sentences) why Lagrange multipliers fail to find the minimum value in this case.

Solution

The method of Lagrange multipliers solves for the point $(x, y)$ at which the tangent line to the curve $g(x, y) = c$ is parallel to the tangent curve to the level curve $f(x, y) = k$. However, at the point $(0, 0)$, the curve $g(x, y) = c$ is ``pointy'' (not smooth) and does not have a well-defined tangent line.

More technically, Lagrange's theorem stipulates the existence of a $\lambda$ if $\nabla g \ne \vec 0$ as it is here. We must therefore also consider these points as candidates for extrema.