Homework 8

Due: March 20, 2018, 8 a.m.

Please give a complete, justified solution to each question below. A single-term answer without explanation will receive no credit.

Please complete each question on its own sheet of paper (or more if necessary), and upload to Gradsescope.

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

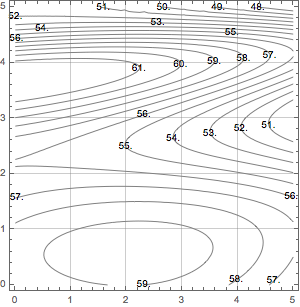
1. The figure below shows the distribution of temperature, in $^\circ$F, in a 5 meter by 5 meter unheated room. Using Riemann sums, estimate the average temperature in the room.

2. Sketch the region of integration (on the $xy$-plane) and evaluate the integral: $$ \int_1^9 \int_{\sqrt{y}}^y x^2 y^3 \ dx \ dy. $$

Then switch the order of integration and write it as a sum of two iterated integrals.

3. If $R$ is the region $\{(x, y) ~|~ x + y \geq a, ~x^2 + y^2 \leq a^2 \}$, with $a > 0$, evaluate the integral $$ \underset{R}{\iint} xy \ dA. $$ Your answer will be in terms of $a$.

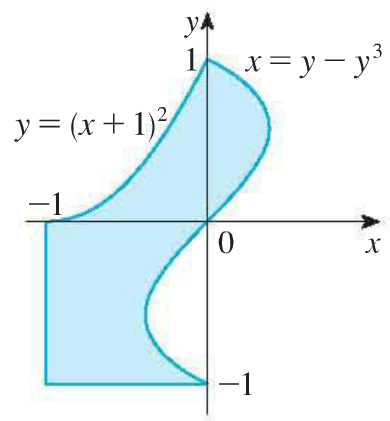
4. Express $D$, the shaded region below, as a union of regions bounded by graphs of functions in the plane, and evaluate the integral $\displaystyle \iint_D y \ dA$.

5.  Sketch the region of integration of $$ \int_0^1 \int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}} x \ dy \ dx + \int_1^2 \int_0^{\sqrt{4-x^2}} x \ dy \ dx $$ and evaluate the integral using polar coordinates.

6. Find the volume of an ice cream cone bounded by the hemisphere $z = \sqrt{8-x^2 - y^2}$ and the cone $z = \sqrt{x^2 + y^2}$. (You could use either polar or Cartesian coordinates.)

7. Sketch and describe the region of integration of the integral below. Include clear explanation/justification.

$$ \int_0^1 \int_{-\sqrt{1-z^2}}^{\sqrt{1-z^2}} \int_0^{\sqrt{1-x^2 - z^2}} f(x, y, z) \ dy \ dx \ dz. $$

8. Evaluate the following triple integral using only geometric interpretation and symmetry: $$ \underset{C}\iiint\ (4 + 5x^2yz^2) \ dV, $$ where $C$ is the cylindrical region: $x^2 + y^2 \leq 4$, $-2 \leq z \leq 2$.