Homework 8 Solutions

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

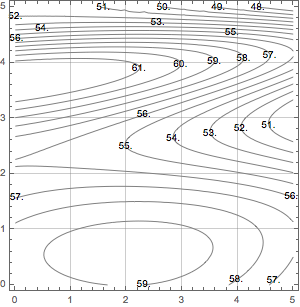
1. The figure below shows the distribution of temperature, in $^\circ$F, in a 5 meter by 5 meter unheated room. Using Riemann sums, estimate the average temperature in the room.

Solution

A sensible sum to take is 25 $1\times 1$ squares in the domain. Each has area $1\text{ m}^2$ and so we need only sum up the temperatures at a sample point of each subrectangle. We'll just look for the contour that passes closest to the center of each square. Reasonable folks can differ on what sample point to use. We approximate. $$T_{\text{avg}} = \frac{1}{\text{area}} \iint_D T(x,y)\,dA \approx \frac{1}{25}\sum_{i=1}^5\sum_{j=1}^5 T\left(\frac{2i-1}{2},\frac{2j-1}{2}\right) \Delta A $$

(moving horizontally from bottom-left)

\begin{align*}\approx \frac{1}{25}( & 59+59+59 + 59 + 57 \

• & 57 + 58 + 58 + 58 + 57 \
• & 56 + 56 + 54 + 53 + 52 \
• & 61 + 61 + 59 + 57 + 53 \
• & 55 + 55 + 55 + 54 + 53) = 56.6^\circ\end{align*}

2. Sketch the region of integration (on the $xy$-plane) and evaluate the integral: $$ \int_1^9 \int_{\sqrt{y}}^y x^2 y^3 \ dx \ dy. $$

Then switch the order of integration and write it as a sum of two iterated integrals.

Solution

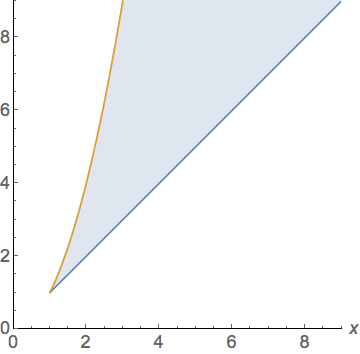
$$ \int_1^3\int_x^{x^2} x^2 y^3\, dy\,dx + \int_3^9\int_x^{9} x^2 y^3\, dy\,dx $$

3. If $R$ is the region $\{(x, y) ~|~ x + y \geq a, ~x^2 + y^2 \leq a^2 \}$, with $a > 0$, evaluate the integral $$ \underset{R}{\iint} xy \ dA. $$ Your answer will be in terms of $a$.

Solution

The two equations intersect at $(0,a)$ and $(a,0)$. Thus, \begin{align*} \int_R xy \ dA &= \int_0^a \int_{a-x}^{\sqrt{a^2 -x^2}} xy \ dy \ dx \\ &= \frac{1}{2} \int_{0}^{a} (a^2 - x^2 -(a-x)^2)x \ dx \\ &= \frac{1}{2} \int_{0}^{a} a^2x - x^3 -a^2x + 2ax^2 - x^3 \ dx \\ &= \frac{1}{2} \bigg(\frac{a^4}{2} - \frac{a^4}{4} - \frac{a^4}{2} + \frac{2a^4}{3} -\frac{a^4}{4}\bigg) \\ &= \frac{a^4}{12} \end{align*}

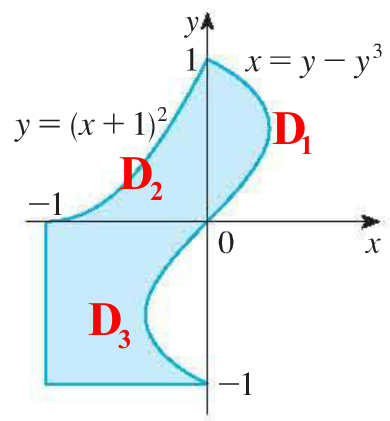
4. Express $D$, the shaded region below, as a union of regions bounded by graphs of functions in the plane, and evaluate the integral $\displaystyle \iint_D y \ dA$.

Solution

\begin{align*} \iint_{D} y \ dA &= \iint_{D_1} y \ dA + \iint_{D_2} y \ dA + \iint_{D_3} y \ dA \\ &= \int_0^1 \int_0^{y-y^3} y \ dx \ dy + \int_{-1}^0 \int_0^{(x+1)^2} y \ dy \ dx + \int_{-1}^0 \int_{-1}^{y-y^3} y \ dx \ dy \\ &= \int_{0}^{1} y(y-y^3) dy + \int_{0}^{-1} \frac{1}{2}(x+1)^4 dx + \int_{-1}^{0} (y(y-y^3) +y)dy \\ &= 2\int_{-1}^{1} y(y-y^3) dy + \int_{0}^{-1} \frac{1}{2}(x+1)^4 dx + \int_{-1}^{0} (y(y-y^3) +y)dy \\ &= 2\bigg( \frac{1}{3} - \frac{1}{5} \bigg) + \frac{1}{2} \bigg( \frac{1}{5} \bigg) - \frac{1}{2} \\ &= -\frac{4}{30} \end{align*}

5.  Sketch the region of integration of $$ \int_0^1 \int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}} x \ dy \ dx + \int_1^2 \int_0^{\sqrt{4-x^2}} x \ dy \ dx $$ and evaluate the integral using polar coordinates.

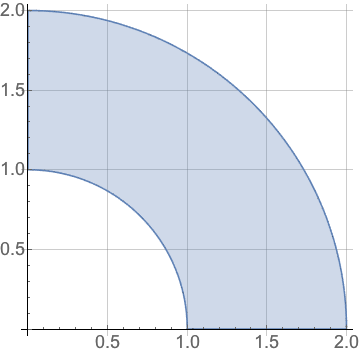
\begin{eqnarray*} \int_0^1 \int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}} x \ dy \ dx + \int_1^2 \int_0^{\sqrt{4-x^2}} x \ dy \ dx & = & \int_0^{\pi/2} \int_{1}^2 r \cos(\theta) \ r \ dr \ d\theta \\ & = & \int_0^{\pi/2} \int_{1}^2 r^2 \cos(\theta) \ dr \ d\theta \\ & = & \int_0^{\pi/2} \left.\frac{r^3}{3}\cos(\theta)\right|_1^2 \ d\theta \\ & = & \int_0^{\pi/2} \frac{7}{3} \cos(\theta) \ d\theta \\ & = & \left. \frac{7}{3} \sin(\theta)\right|_0^{\pi/2} = \frac{7}{3}. \end{eqnarray*}

6. Find the volume of an ice cream cone bounded by the hemisphere $z = \sqrt{8-x^2 - y^2}$ and the cone $z = \sqrt{x^2 + y^2}$. (You could use either polar or Cartesian coordinates.)

Solution

First, find the intersection between the hemisphere and the ice cream cone: $$ 8 - x^2 - y^2 = x^2 + y^2, ~ z = \sqrt{x^2 + y^2} $$ or equivalently, $$ x^2 + y^2 = 4, ~ z = 2$$ a circle of radius 2 parallel to the $xy$-plane, centered at $(0, 0, 2)$.

So, the region of integration, call it $D$, should be the circle of radius 2 in the $xy$-plane, centered at the origin. The equation in polar coordinate is: $r = 2$, $0 \leq \theta \leq 2$. The integrand should be the $z$-range so that for each $(x, y)$, the point $(x, y, z)$ is inside the ice cream cone: [ \sqrt{x^2 + y^2} \leq z \leq \sqrt{8 - x^2 - y^2}. ] Therefore, the volume is: \begin{eqnarray*} \iint_D \sqrt{8 - x^2 - y^2} - \sqrt{x^2 + y^2} \ dA & = & \int_0^{2\pi} \int_{0}^2 (\sqrt{8-r^2} - r) \ r \ dr \ d\theta \\ & = & \int_0^{2\pi} \int_{0}^2 \sqrt{8-r^2} \ r \ dr \ d\theta - \int_0^{2\pi} \int_{0}^2 r^2 \ dr \ d\theta\\ & = & \frac{32\pi}{3}(\sqrt{2}-1). \end{eqnarray*}

7. Sketch and describe the region of integration of the integral below. Include clear explanation/justification.

$$ \int_0^1 \int_{-\sqrt{1-z^2}}^{\sqrt{1-z^2}} \int_0^{\sqrt{1-x^2 - z^2}} f(x, y, z) \ dy \ dx \ dz. $$

Solution

$0 \leq z \leq 1, \ -\sqrt{1-z^2} \leq x \leq \sqrt{1-z^2} \Leftrightarrow 0 \leq x^2 + z^2 \leq 1, \ 0 \leq y \leq \sqrt{1-x^2 - z^2} \Leftrightarrow 0 \leq x^2 + y^2 + z^2 \leq 1$. Combine the three inequalities, then

8. Evaluate the following triple integral using only geometric interpretation and symmetry: $$ \underset{C}\iiint\ (4 + 5x^2yz^2) \ dV, $$ where $C$ is the cylindrical region: $x^2 + y^2 \leq 4$, $-2 \leq z \leq 2$.

Solution

Split the integral into the sum of two integrals over $C$: $$ \iiint_{C} 4 \ dV + 5\iiint_{C} x^2yz^2 \ dV. $$ Note that $\iiint_{C} 4 \ dV = 4 \iiint_{C} 1 \ dV = $ 4 times the volume of $C$. Since $C$ is a cylinder, its volume is the area of the base (circle of radius 2) with its height (4), namely $4 \times 2^2 \pi \times 4 = 64 \pi$.

Consider the second integral, $\iiint_{C} x^2yz^2 \ dV$. Note that the cylinder $C$ is symmetric about the $xz$-plane: if the point $(x, y, z)$ is in the cylinder $C$, then $(x, -y, z)$ is also in $C$. On the other hand, the function $f(x, y, z) = x^2y z^2$ is odd with respect to $y$: $$ f(x, -y, z) = - f(x, y, z). $$ Let $C_1$ denote the part of $C$ that has negative $y$ components and $C_2$ the part of $C$ that has negative $y$ components. Then, \begin{eqnarray*} \iiint_C f(x, y, z)\ dV & = & \iiint_{C_1} f(x, y, z) \ dV + \iiint_{C_2} f(x, y, z) \ dV \\ & = & \iiint_{C_1} f(x, y, z) \ dV - \iiint_{C_1} f(x, y, z) \ dV = 0. \end{eqnarray*}

So, $\iiint_{C} (4 + 5x^2yz^2) \ dV = \iiint_{C} 4 \ dV = 64\pi$.