Homework 9 Solution

$$ \newcommand{\R}{\mathbb{R}} \newcommand{\dydx}{\frac{dy}{dx}} \newcommand{\proj}{\textrm{proj}} % For boldface vectors: \renewcommand{\vec}[1]{\mathbf{#1}} $$

1. Sketch the region of integration of the of the following iterated integral and then re-express it in "$dx\,dz\,dy$" order.

$$ \int_{-1}^0\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_0^{y+2} f(x,y,z) \,dz\, dy\, dx $$ Finally, reexpress it in cylindrical coordinates.

Solution

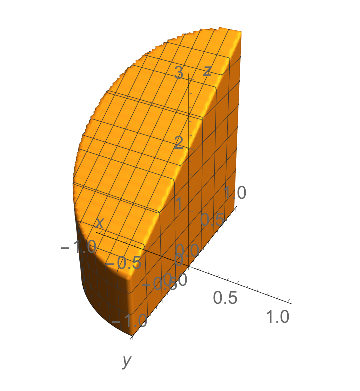
$$ \int_{-1}^1\int_0^{y+2} \int_{-\sqrt{1-y^2}}^{0} f(x,y,z) \,dx\, dz\, dy $$ Finally, reexpress it in cylindrical coordinates.

$$ \int_{\pi/2}^{3\pi/2}\int_0^{1} \int_{0}^{r\sin\theta+2} f(r \cos \theta,r\sin \theta,z) r\,dz\, dr\, d\theta $$

2. Find the volume of the following "stadium" using spherical coordinates. The "inner" wall is a piece of a sphere of radius 2; the "stands" are part of the cone $z^2=x^2+y^2$.

Solution

In spherical coordinates, $\rho$ is bounded on the inside by 2, but by the walls of the cylinder on the outside, so the upper bound of $\rho$ varies with $\phi$. We therefore solve on this boundary $r=\rho \sin \phi = 4$ or $\rho = 4\csc \phi$.

We therefore have the integral
$$ \int_{\pi/2}^{2\pi} \int_{\pi/4}^{\pi/2} \int_2^{4\csc \phi} \rho^2 \sin \phi\,d\rho \,d\phi\,\theta $$ or alternatively, by filling in the "anticone", evaluating the volume with cylindrical coords and subtracting the inner spherical part, we get two easier integrals $$ \int_{\pi/2}^{2\pi}\int_0^4\int_0^r r \,dz\,dr\,d\theta - \int_{\pi/2}^{2\pi} \int_{\pi/4}^{\pi/2} \int_0^2 \rho^2 \sin \phi\,d\rho \,d\phi\,\theta $$

Both yield the answer $\left(32-2\sqrt{2}\right)\pi$.

3. Find the center of mass $(\overline{x},\overline{y},\overline{z})$ of the "ice cream cone" from homework 8 (that is the region above the cone $z=\sqrt{x^2+y^2}$ and inside the sqphere $x^2+y^2+z^2=8$). Assume the ice cream has uniform density.

Hint: You may reason your way to 2 of the coordinates without computing anything directly, but you must set up and evaluate an integral (or integrals) for the third.

Solution

This region clearly has radial symmetry about the $z$-axis, and so without computation we can conclude $\bar{x}=\bar{y}=0$. We thus need to compute only $$\bar{z} = \frac{\iiint_E z \rho(x,y,z)\,dV}{\iiint_E \rho(x,y,z)\,dV}. $$

The density $\rho$ is constant here and so will cancel out in the quotient above. The region is easiest described in spherical coordinates.

$$ \text{volume} = \int_{0}^{2\pi} \int_0^{\pi/4} \int_0^{2\sqrt2} \rho^2 \sin\phi\,d\rho\,d\phi\,d\theta = \frac{32}{3} \left(\sqrt{2}-1\right) \pi $$

$$ \text{moment} = \int_{0}^{2\pi} \int_0^{\pi/4} \int_0^{2\sqrt2} (\rho\cos\phi) \rho^2 \sin\phi\,d\rho\,d\phi\,d\theta = 8\pi $$

So $\bar{z}\approx 1.81$.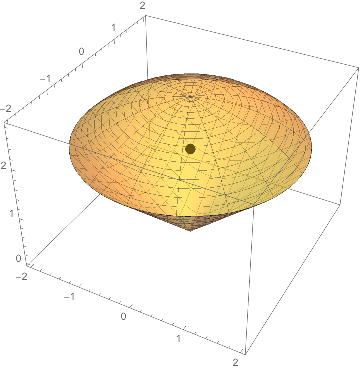

4. Repeat question 3 but assume the ice cream in the cone (i.e., that below the rim) is twice as dense as that above.

Solution

The difference here is that $\rho$ is piecewise defined so we can just split the integral above between the region in the cone and "above" it.

\begin{align*} \text{volume} &= \int_{0}^{2\pi} \int_0^{\pi/4} \int_0^{2\sec\phi} 2 \rho^2 \sin\phi\,d\rho\,d\phi\,d\theta \\ & + \int_{0}^{2\pi} \int_0^{\pi/4} \int_{2\sec\phi}^{2\sqrt2} \rho^2 \sin\phi\,d\rho\,d\phi\,d\theta \\ &= \frac{32 \sqrt{2} \pi }{3}-8 \pi \end{align*}

\begin{align*} \text{moment} &= \int_{0}^{2\pi} \int_0^{\pi/4} \int_0^{2\sec\phi} 2 \rho^3 \sin\phi\cos\phi\,d\rho\,d\phi\,d\theta \\ & + \int_{0}^{2\pi} \int_0^{\pi/4} \int_{2\sec\phi}^{2\sqrt2} \rho^3 \sin\phi\cos\phi\,d\rho\,d\phi\,d\theta \\ &= 12\pi \end{align*}

So $\bar{z}\approx 1.69$.