Lecture 04
Intro to Curves
APMA E2000
Drew Youngren dcy2@columbia.edu
Announcements
-
Quiz 1 (HW1 topics) today.
- HW1 topics
- 10 minutes at end of lecture
- HW2 due next Tues
1-minute review
Lines
A line in $\RR^n$ with position $\vec p$ and direction $\vec v$ has parametric form \[ \vec r(t) = \vec p + t\,\vec v \]
Planes
A plane in $\RR^3$ with position vector $\vec p$ and normal vector $\vec n$ has plane equation \[ \vec n \cdot (\vec x - \vec p) = 0.\]
Distances
Definition
The distance between sets is defined as the minimum of all distances between points in the respective sets. \[ \operatorname{dist}(X,Y) = \operatorname{min}\limits_{\vec x \in X, \vec y \in Y} |\vec x - \vec y| \]
Point-to-Plane
Find the distance from a position $\vec y$ to a plane with normal $\vec n$ and position $\vec p$.
Skew Lines
Find the distance between skew lines \[\bv{ - t \\ t \\ 1 } \text{ and } \bv{ 1 - t \\ 1 + 2t \\ 2 + t}.\]
Space Curves
Definition
A curve in $\RR^n$ is the image of a
vector-valued function
$\vec r: \RR \to \RR^n$.
It has the form \[ \vec r(t) = \left\langle x(t), y(t), z(t) \right\rangle. \]
Examples
- Twisted Cubic: $\left\langle t, t^2, t^3 \right\rangle$
- Helix: $\left\langle \cos(t), \sin(t), t \right\rangle$
- Wacky: $\left\langle \cos(8 t), \sin(3 t), \sin(7 t) \right\rangle$
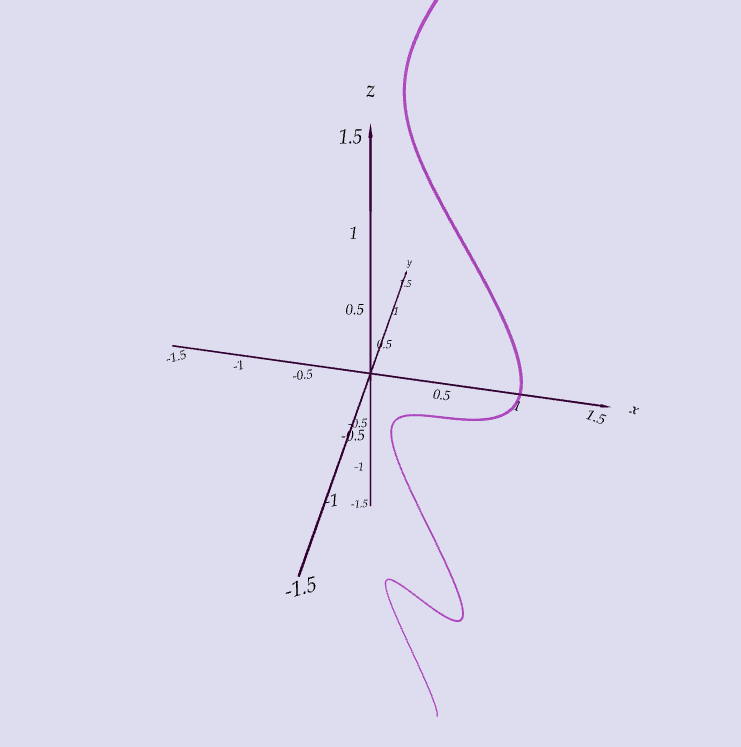
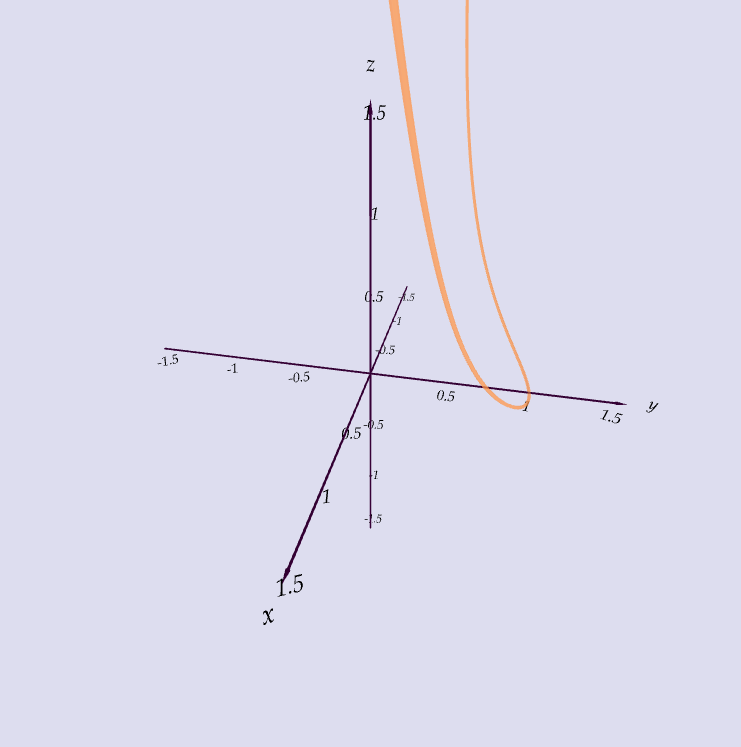
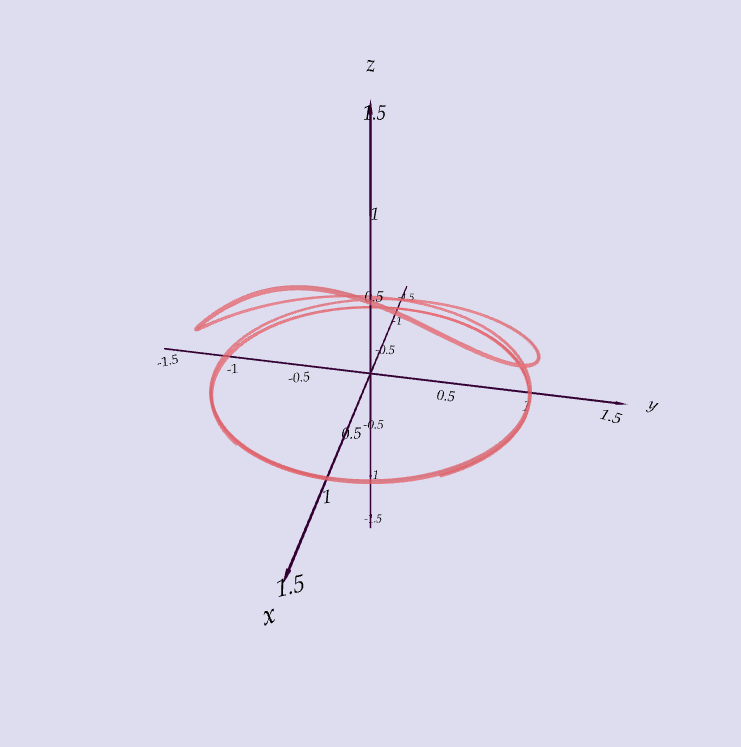
Exercise
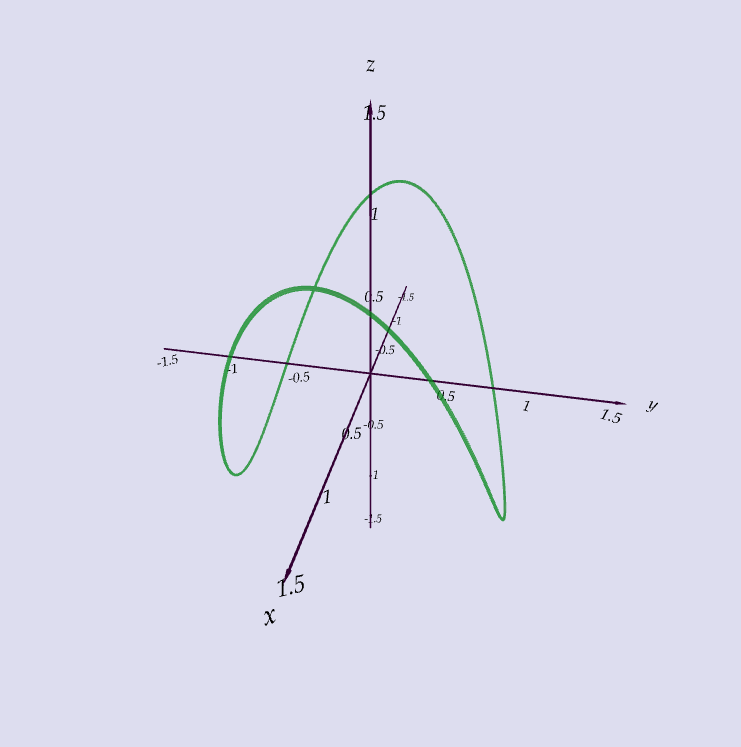
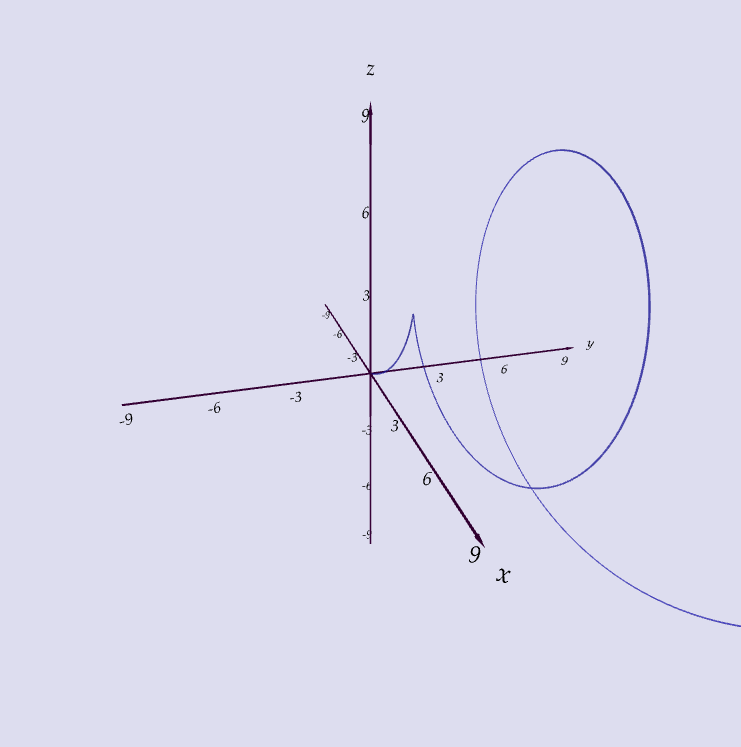
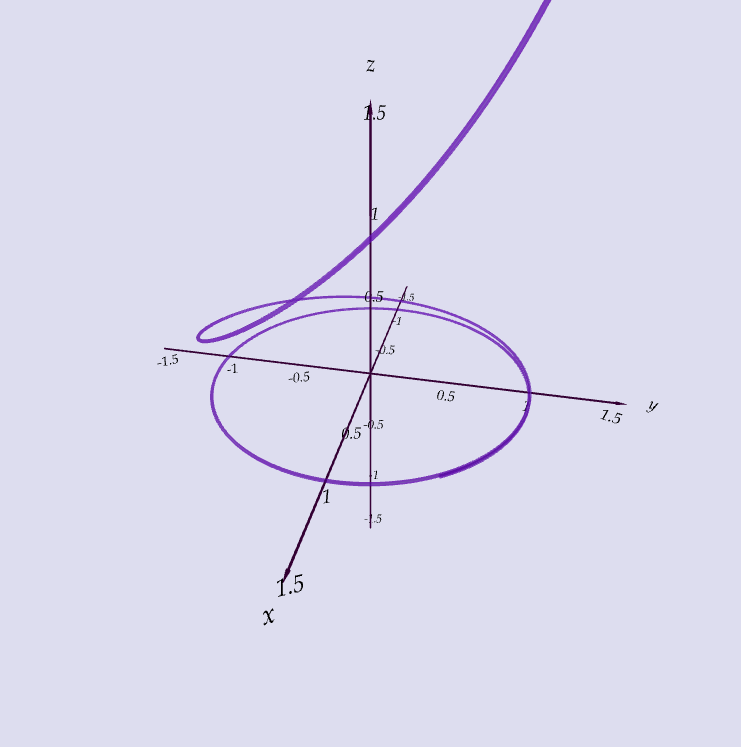
Which curve is which?
| A. $\langle t \cos t, t, t\sin t\rangle$ |
| B. $\langle \cos t, \sin t, 1/(1+t^2)\rangle$ |
| C. $\langle t, 1/(1+t^2),t^2\rangle$ |
| D. $\langle \cos t, \sin t, \cos 2t\rangle$ |
| E. $\langle \cos 8t, \sin 8t, e^{0.8t}\rangle$ |
| F. $\langle \cos^2 t, \sin^2 t, t\rangle$ |
Example
Find a parametrization of the intersection of the cylinder $x^2 + y^2 = 4$ and the plane $x - 2y +4z = 2$.
Solution. Parametrize the circle of radius 2 to get $x(t) = 2 \cos t$ and $y = 2 \sin t$. Then solve for $z$ in the plane equation. \[\vec r(t) = \langle 2 \cos t, y = 2 \sin t, \frac14(2-2\cos t + 4\sin t) \rangle.\]
Calculus
Finally.
Limits
\[\lim_{t \to a} \vec r(t) = \vec L\]Limits
\[\lim_{t \to a} \vec r(t) = \bv{\lim_{t \to a} x(t) \\ \lim_{t \to a} y(t) \\ \lim_{t \to a} z(t) \\ }\]Derivatives
The derivative of a vector-valued function is defined exactly as in one-variable calculus, as a limit of a difference quotient.
\[\vec r'(a) = \lim_{t \to a} \frac{\vec r(t) - \vec r(a)}{t - a} \]Example
Where does the tangent line to the curve $\langle t, t^2, t^3 \rangle$ at $(1,1,1)$ intersect the $xy$-plane?
Solution. First, note $\vec r(1) = \langle 1,1,1 \rangle$ and $\vec r'(1) = \langle 1,2,3 \rangle$ are position and direction vectors for the tangent line. We therefore solve \[\bv{1 + s \\ 1 + 2s \\ 1 + 3s} = \bv{x \\ y \\ 0}.\]
Learning Outcomes
You should be able to...
- Formulate the Fundamental Theorem of Calculus for vector-valued functions.
- Identify position, velocity, speed, and acceleration using the machinery of vector-valued functions.
- Solve initial-value motion problems with piecewise-defined acceleration functions.
- Try your hand at the silly rocket game.