Lecture 18

FTLI

APMA E2000

Drew Youngren dcy2@columbia.edu bb

$\gdef\RR{\mathbb{R}}$ $\gdef\vec{\mathbf}$ $\gdef\bv#1{\begin{bmatrix} #1 \end{bmatrix}}$ $\gdef\proj{\operatorname{proj}}$ $\gdef\comp{\operatorname{comp}}$

Announcements

  • HW 10 due Tues (after exam)
  • No quiz this week
  • Recitation as usual

1-minute review

Path Integral

Let $C$ be a smooth curve parametrized by $\vec r(t) = \langle x(t), y(t) \rangle, a \leq t \leq b$ and $\vec F(x,y) = \langle P(x,y), Q(x,y) \rangle$.

\[ \int\limits_C \vec F\cdot d\vec r = \int\limits_C P\,dx + Q\,dy = \int\limits_C \vec F\cdot\vec T\,ds \]
\[ = \int_a^b (P(x(t), y(t)) x'(t)+ Q(x(t), y(t)) y'(t))\,dt \]
Example

Compute \[\int\limits_C (x-y)\,dx + xy\,dy\] where $C$ is the portion of the clockwise-oriented unit circle from $(1,0)$ to $(0, 1)$.

Plot of vector field with oriented curve.

Solution. $\vec r(t) = \langle \cos t, -\sin t \rangle, 0 \leq t \leq \frac{3\pi}{2}$. We compute

\[ \int_0^{3\pi/2} (\cos t + \sin t)(-\sin t) + (\cos t)(\sin t)\cos t\,dt \]\[ = -\frac{1}{6}-\frac{3 \pi }{4}\]

← Work Integral

A wagon is pulled across the floor by a rope 5 meters away and 1 meter up with a force of 7 N. Find the work done. (The wagon weighs more than 7 N.)

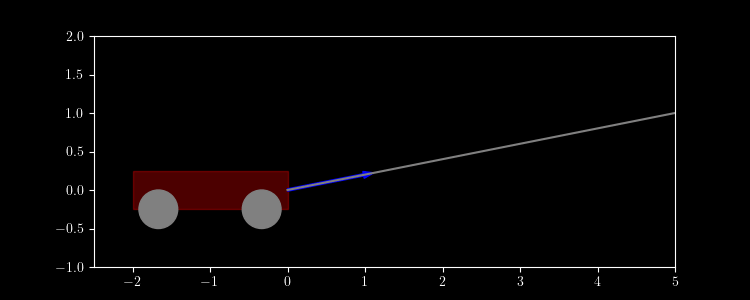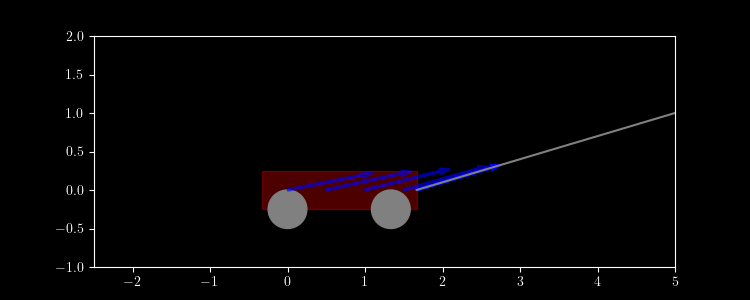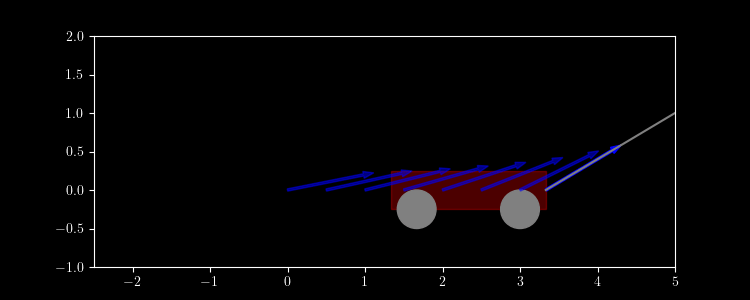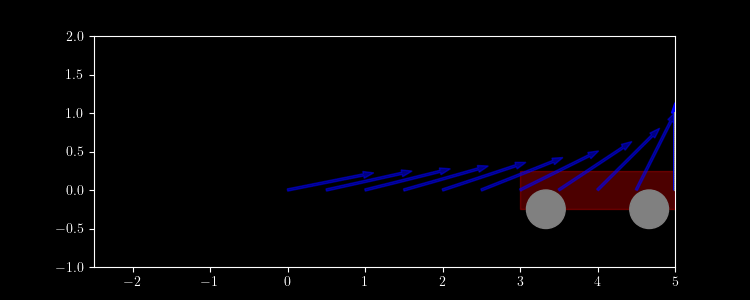
GIF of wagon being pulled with force vectors plotted.

Solution. $\vec r(t) = \langle t, 0 \rangle, 0 \leq t \leq 5$. \[\vec F(x,y) = 7\frac{\langle 5, 1 \rangle - \langle x, y \rangle}{|\langle 5, 1 \rangle - \langle x, y \rangle|} \] \[ W = \int_0^5 7\frac{5 - t}{\sqrt{1 + (5 - t)^2}}\,dt \approx 28.7\, \text{N}\text{m} \]

Conservative Vector Fields

Definition

A vector field $\vec F$ is conservative if there is a scalar field $f$ (called a potential) where \[\vec F = \nabla f.\]

Example

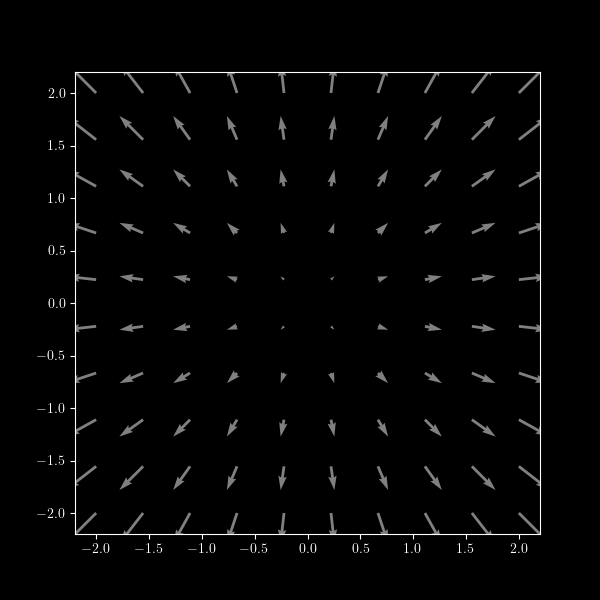
The radial vector field $x \,\vec i + y\, \vec j$ is conservative. Its potential is

\[f(x,y) = \frac{x^2 + y ^2}{2}\]

A radial vector field.
Example

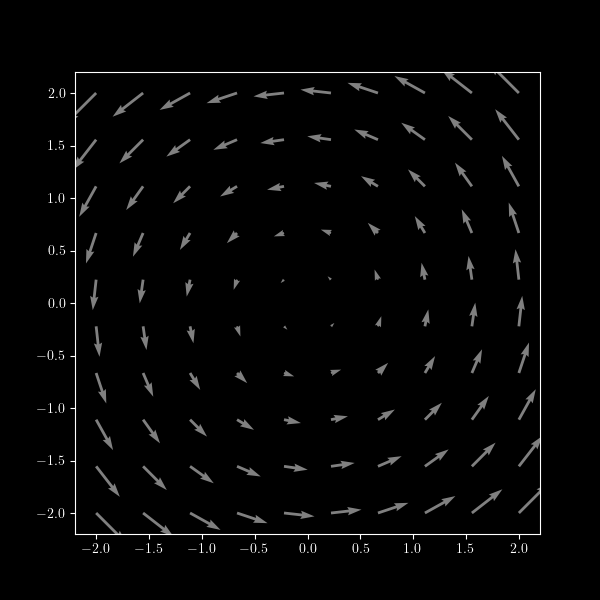
The vector field \[ -y\,\vec i + x\,\vec j \] is not conservative.

A circular vector field.
Test for Conservativeness

If $\vec F = \langle P, Q \rangle$ is a conservative vector field \[P_y = Q_x.\]

Proof. Suppose $\vec F = \langle P, Q \rangle = \nabla f$. \[P_y = f_{xy} = f_{yx} = Q_x .\]

Example

Determine whether each of the following is conservative, and if so, find a potential function.

\[ \vec F(x,y) = \langle y e^{xy}, x e^{xy} + y^3 \rangle \]

Conservative. $\displaystyle f(x,y) = e^{xy} + \frac14y^4$

Example

Determine whether each of the following is conservative, and if so, find a potential function.

\[ \vec F(x,y) = \langle xy, xy \rangle \]

Not conservative. $\displaystyle P_y = x \neq Q_x = y$

Example

Determine whether each of the following is conservative, and if so, find a potential function.

\[ \vec F(x,y,z) = \langle y + z, x + z, x + y + z \rangle \]

Conservative. $\displaystyle f(x,y,z) = xy + xz + yz + \frac12 z^2$

A Fundamental Theorem

Let's compute a path integral of a conservative vector field.

\[ \int\limits_C \nabla f \cdot d\vec r\]

with the usual definitions, \[ = \int_a^b \nabla f(\vec r(t)) \cdot \vec r'(t)\,dt \]

\[ = \int_a^b \frac{d}{dt}(f\circ \vec r )(t)\,dt = f(\vec r(b)) - f(\vec r(a)) \]

Fundamental Theorem of Line Integrals

If $\vec F = \nabla f$ and $C$ is a continuous path from $P_0$ to $P_1$, then \[\int\limits_C \vec F\cdot d\vec r = f(P_1) - f(P_0).\]

Corollary. If $C$ is a closed curve, \[ \oint\limits_C \nabla f\cdot d\vec r = 0 \]

Example

Compute the work done against gravity carrying a 15 lbs bowling ball up a helical ramp 70 ft high.

Solution

$\vec F = \langle 0, 0, 15 \rangle = \nabla (15z)$ \[ W = \int_C \vec F\cdot d\vec r = 15(70) - 15(0) = 1050 \text{lbs}\cdot\text{ft} \]

Example

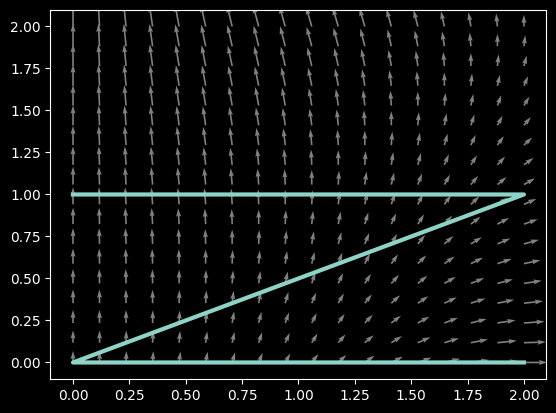
Compute the line integral \[\int_C (x^2 - xy)\,dx + (y- \frac{x^2}{2} + 2)\,dy \] where $C$ is the polygonal path from $(2,0)$ to $(0,0)$ to $(2,1)$ to $(0,1)$.

Z-shaped path in a vector field
Conservation of Energy

Suppose a force is given by $\vec F = -\nabla f$ and a particle of mass $m$ traverses a path $\vec r(t), a \leq t \leq b$.

\[ \text{W} = \int\limits_C \vec F\cdot d\vec r\]
Conservation of Energy

Suppose a force is given by $\vec F = -\nabla f$ and a particle of mass $m$ traverses a path $\vec r(t), a \leq t \leq b$.

\[ \text{W} = \int\limits_C \vec F\cdot d\vec r = f(\vec r(a)) - f(\vec r(b))\]
Conservation of Energy

Suppose a force is given by $\vec F = -\nabla f$ and a particle of mass $m$ traverses a path $\vec r(t), a \leq t \leq b$.

\[ \begin{align*}\text{W} &= \int_a^b m\vec r''(t)\cdot \vec r'(t)\,dt \\ &= \int_a^b \frac{d}{dt}\left(\frac12 m \vec r'(t) \cdot \vec r'(t) \right)\,dt \\ &= \frac12 m |\vec r'(b)|^2 - \frac12 m |\vec r'(a)|^2 \end{align*}\]
Conservation of Energy

Suppose a force is given by $\vec F = -\nabla f$ and a particle of mass $m$ traverses a path $\vec r(t), a \leq t \leq b$.

\[ \frac12 m |\vec r'(b)|^2 + f(\vec r(b)) = \frac12 m |\vec r'(a)|^2 + f(\vec r(a)) \]
Escape Velocity

The Gravitational force from a mass $M$ at the origin on a mass $m$ at position $\vec x$ is \[ \vec G = -\frac{GMm \vec x}{|\vec x|^3}. \] Find the work done moving an object from the surface of the earth to the end of the universe.

On Earth
\[\begin{align*}G &= 6.674 \times 10^{-11} \frac{\text{N}\text{m}^2}{\text{kg}^2} \\ M &= 5.97\times10^{24} \text{kg} \\ R &= 6.371\times 10^{6} \text{m} \end{align*}\] Escape velocity is $\sqrt{\frac{2GM}{R}} = 11183.9 \frac{\text{m}}{\text{s}}$.

Learning Outcomes

You should be able to...
  • Interpret a line integral of a vector field as sum of line integrals of scalar fields.
  • Determine if a vector field is conservative and find a potential if so.
  • Recognize when and how to apply FTLI.
  • Equate path-independence with closed loops yielding 0.
  • Solve mechanical problems with conservative forces.